HankelMatrix[n]
第1行と第1列が連続する整数である n×n のハンケル(Hankel)行列を返す.
HankelMatrix[{c1,c2,…,cn}]
第1列が成分 c1, c2, … からなるハンケル行列を返す.
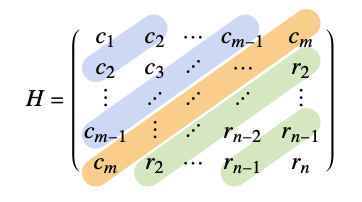
HankelMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
第1列の成分が ci,最終行の成分が riのハンケル行列を返す.


HankelMatrix
HankelMatrix[n]
第1行と第1列が連続する整数である n×n のハンケル(Hankel)行列を返す.
HankelMatrix[{c1,c2,…,cn}]
第1列が成分 c1, c2, … からなるハンケル行列を返す.
HankelMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
第1列の成分が ci,最終行の成分が riのハンケル行列を返す.
詳細とオプション


- ハンケル行列は,通常,近似理論,関数解析,数値解析,信号処理等に関連した応用で使われる.
- ハンケル行列は,その反対角行列に沿って一定の行列である.ハンケル行列
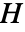 の成分は,
の成分は,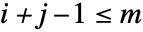 のときは
のときは 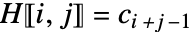 で,それ以外のときは
で,それ以外のときは  で与えられる.
で与えられる. - 成分 cmは r1と同じでなければならない. »
- m=n のとき,ハンケル行列は対称行列で,成分 ciと rjが実数なら実固有値を持つ.
- HankelMatrix[…,TargetStructure->struct]はハンケル行列を struct で指定された形式で返す.次は,その可能な設定である.
-
Automatic 返す際の表現を自動選択する "Dense" 行列を密な行列として表す "Structured" 行列を構造化配列として表す "Symmetric" 行列を対称行列として表す - HankelMatrix[…,TargetStructureAutomatic]の設定では,行列の成分数が設定された閾値未満の場合は密な行列が返され,それ以外の場合は構造化配列が返される.
- 構造化されたHankelMatrix sa は,次の特性"prop"に sa["prop"]でアクセスできる.
-
"ColumnVector" 第1列の成分のベクトル "RowVector" 最終行の成分のベクトル "Properties" サポートされる特性のリスト "Structure" 構造化配列の型 "StructuredData" 構造化配列で保存されている内部データ "StructuredAlgorithms" 構造化配列に対して特別なメソッドを持つ関数のリスト "Summary" Datasetとして表される要約情報 - Normal[HankelMatrix[…]]は構造化ハンケル行列を通常の行列に変換する.
例題
すべて開く すべて閉じるスコープ (9)
HankelMatrixオブジェクトには配列についての情報を与える特性が含まれる:
"ColumnVector"特性はハンケル行列の第1列を与える:
"Summary"特性は配列についての情報の簡単な要約を与える:
"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数のリストを与える:
構造化アルゴリズムは,適切な場合は別のHankelMatrixオブジェクトを返す:
転置もまたHankelMatrixである:
オプション (2)
TargetStructure (2)
TargetStructureAutomaticの設定のとき,小さい次元については密な行列が返される:
アプリケーション (4)
![]() 次パデ(Padé)近似はハンケル行列式を使って計算できる.Exp[z]のベキ級数の最初の 2n+1の部分和を生成する:
次パデ(Padé)近似はハンケル行列式を使って計算できる.Exp[z]のベキ級数の最初の 2n+1の部分和を生成する:
Shanks変換は,![]() 次パデ近似を2つのハンケル行列式の比として表す:
次パデ近似を2つのハンケル行列式の比として表す:
PadeApproximantの結果と比較する:
プロニー法(Prony's method)[Wikipedia]を使ってデータから指数関数の和を回復する:
ハンケル行列の行列式は関数の連分数展開に現れる.関数の最初のいくつかの級数展開の係数を生成する:
級数係数からハンケル行列式を構築するための効用関数を定義する:
区間![]() 上の重み関数
上の重み関数 ![]() に対応する n 点のガウス求積法は重み関数のモーメントから導出できる.重み関数と区間を定義する:
に対応する n 点のガウス求積法は重み関数のモーメントから導出できる.重み関数と区間を定義する:
指定された重み関数に対応する n 次直交多項式は,モーメントから構築されたハンケル系を解くことで入手できる:
n 点ガウス求積法の重みは,Vandermonde系を解くことで入手できる:
NIntegrateで得られた答と比較する:
特性と関係 (6)
HankelMatrix[c,RotateRight[c]]は正方の反循環行列である:
正方反循環行列は固有値 c1+c2+…の固有ベクトル{1,…}を持つ:
HankelMatrixとToeplitzMatrixは,交換行列 (逆恒等行列) との乗算によって関連している:
同様に,ハンケル行列の逆変換はテプリッツ(Toeplitz)行列を与える:
テキスト
Wolfram Research (2007), HankelMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/HankelMatrix.html (2024年に更新).
CMS
Wolfram Language. 2007. "HankelMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/HankelMatrix.html.
APA
Wolfram Language. (2007). HankelMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HankelMatrix.html
BibTeX
@misc{reference.wolfram_2025_hankelmatrix, author="Wolfram Research", title="{HankelMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HankelMatrix.html}", note=[Accessed: 11-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_hankelmatrix, organization={Wolfram Research}, title={HankelMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HankelMatrix.html}, note=[Accessed: 11-February-2026]}