HiddenMarkovProcess
HiddenMarkovProcess[i0,m,em]
表示一个离散时间、有限状态的隐马尔可夫过程,该过程包括转换矩阵 m,输出矩阵 em 和初始隐含状态 i0.
HiddenMarkovProcess[…,m,{dist1,…}]
表示一个输出分布为 disti 的隐马尔可夫过程.
HiddenMarkovProcess[p0,m,…]
表示一个初始隐含状态概率矢量为 p0 的隐马尔可夫过程.
更多信息



- HiddenMarkovProcess 亦称为隐马尔可夫模型或 HMM.
- HiddenMarkovProcess 是一个离散时间和离散状态的随机过程.
- 隐马尔可夫过程以 DiscreteMarkovProcess[p0,m] 作为底层的隐含状态转换过程. 从一个隐马尔可夫过程观察到的值,即输出,是随机的,在状态为 i 时服从输出分布 disti. 访问给定状态序列所产生的输出是独立的.
- HiddenMarkovProcess 的隐含状态是一些介于 1 和
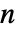 之间的整数,其中
之间的整数,其中 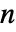 是转换矩阵 m 的长度.
是转换矩阵 m 的长度. - 转换矩阵 m 指定了有条件的隐含状态转换概率 m〚i,j〛Probability[x[k+1]jx[k]i],其中 x[k] 是时间 k 时过程的隐含状态.
- 输出矩阵 em 规定了在特定隐含状态下输出的概率 em〚i,r〛Probability[y[k]rx[k]i],其中 x[k] 是隐含状态,y[k] 是时间 k 时的输出.
- 输出分布 disti 必须全部是单变量的或者全部是多变量的,全部是离散的或者全部是连续的.
- 输出分布 disti 规定如果 x[k]i,则 y[k]disti.
- 在输出矩阵中,可以用一行零表示一个无输出的静止状态,对于一般输出,也可用 None 来表示. 每个静止状态必须有一条路径通往一个输出状态.
- 对于含有静止状态的隐马尔可夫过程 proc, HiddenMarkovProcess[proc] 会给出不包含静止状态的有效过程.
- EstimatedProcess[data,HiddenMarkovProcess[n,edist]] 可被用于估算有 n 个状态的过程,其中输出分布属于由 edist 指定的分布组合.
- 可使用下列特殊 edist 模板:
-
s s 离散输出 "Gaussian" 高斯输出 dist 分布为 dist 的状态的输出 {dist1,…,distn} 状态 i 的输出分布 disti - EstimatedProcess 可接受下列关于 ProcessEstimator 的设置:
-
Automatic 自动选择参数估算器 "BaumWelch" 期望最大化算法的最大化对数似然 "ViterbiTraining" 解码最可能的路径以及采用有监督训练 "StateClustering" 先用聚类算法然后用有监督训练 "SupervisedTraining" 根据状态和输出数据来估计 - 方法 "BaumWelch"、"ViterbiTraining" 和 "StateClustering" 不要求指定估计中的隐含状态路径,而 "SupervisedTraining" 却要求访问隐藏的状态路径数据.
- 对数据进行运算的函数,比如 LogLikelihood 可接受 Missing 值.
- 默认情况下,RandomFunction[HiddenMarkovProcess[…]] 只给出输出. 如果设置 Method->{"IncludeHiddenStates"->True},函数将给出一个 TemporalData 对象 td,同时,还包括状态序列作为元数据. 可以利用 td["HiddenStates"] 来提取隐含状态数据.
- HiddenMarkovProcess 规定 m 是
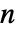 ×
×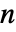 的矩阵,元素非负,每行元素之和为1,em 为
的矩阵,元素非负,每行元素之和为1,em 为 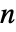 ×
×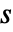 的矩阵,元素非负,每行元素之和为 0 或 1, i0 是介于 1 和
的矩阵,元素非负,每行元素之和为 0 或 1, i0 是介于 1 和 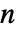 之间的整数,p0 是长度为
之间的整数,p0 是长度为 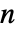 的矢量,元素非负,元素之和为 1.
的矢量,元素非负,元素之和为 1. - HiddenMarkovProcess 可以与某些函数一起使用,比如 LogLikelihood、 FindHiddenMarkovStates、EstimatedProcess、PDF、 Probability 以及 RandomFunction 函数.
范例
打开所有单元关闭所有单元范围 (17)
基本用法 (8)
计算一个输出序列的 LogLikelihood:
用 None 或零矢量来表示静止状态:
用 None 来表示静止状态:
使用带有 Property 注记的 Graph 来定义 HiddenMarkovProcess:
估算 (5)
过程内部属性 (4)
推广和延伸 (1)
应用 (11)
游戏 (3)
某个偶尔不老实的赌场提供一种赌硬币游戏,使用欺诈手段在所用的硬币上做了手脚,头出现的概率是尾出现概率的三倍. 已知赌场发牌员在悄悄的交替使用正常的硬币和有问题的硬币,概率为 10%:
有一个人,每次随机的选择一个瓮,取出一个球,报告球的颜色,然后把球放回其中一个瓮里. 如此重复四次. 转移到下一个瓮的概率为:
出现颜色序列为 {red,blue,green,green} 的概率:
在第一人称射击游戏中,一个特工隐藏在某一关中,等着跳出来攻击玩家. 该特工看不到玩家,但可以听到他们在做什么,结合他所知的游戏布局来估计玩家的位置. 假设这样一个布局,有27个区,四种类型——草地、金属栅板、水和门户:
遗传学 (3)
一个 DNA 序列是由碱基 A、C、G、和 T 组成的. 名为核苷酸序列的子序列则是以每个字母出现的不同频率来区分开的. 一个重要的任务是将 DNA 序列分成不同的核苷酸子序列. 设想我们有一个 DNA 序列,以一个外显子开始,包含一个 5’ 剪接位点,结束于一个内含子. 如果外显子的碱基组成是均匀的,内含子缺少 C 和 G 碱基对,剪接位点共有核苷酸序列的 G 碱基概率是 0.95. 那么,核苷酸频率的分布为:
状态机的状态为外显子 (1)、剪接位点 (2)、内含子 (3) 和终端 (4),状态间的转换概率为:
输出结果为核苷酸 A (1)、C (2)、G (3)、T (4) 或终端 (5):
找到给予核苷酸序列最可能在的位置(外显子、剪接位点、内含子或终端):
模式种乳腺癌的风险是因为遗传了 BRCA1 基因的一个受损的等位基因 B 而导致的. 遗传过程中,父母各自贡献自己的两个等位基因中的一个,那么每个等位基因就有 1/2 被遗传的概率:
如果母亲有一对正常的等位基因 “bb”,那么该父母的儿子可能出现的各个等位基因组合的概率为:
这个男孩的输出概率跟他的父亲是一样的,因为他们都是男性. 输出结果 1 意味着癌症,2 意味着没有癌症:
这是一种自花授粉的植物,也就是说,子代的基因型只取决于父代的基因型:
用 DiscreteMarkovProcess 来对各代之间的基因型改变建模:
等位基因决定植物的表现型,即可见的特征。假设大写字母代表的等位基因相对对应的小写字母代表的等位基因是完全显性的:
天气 (2)
属性和关系 (6)
带有离散输出的 HiddenMarkovProcess 的 SliceDistribution 的计算结果为经验分布 DataDistribution:
找出时间 ![]() 和
和 ![]() 时输出的联合分布的 PDF:
时输出的联合分布的 PDF:
在任何单个时间,带有指数输出的 HiddenMarkovProcess 的输出遵从 HyperexponentialDistribution:
带有一般输出分布的 HiddenMarkovProcess 的输出结果为 MixtureDistribution:
HiddenMarkovProcess 被定义来重新标记隐含状态:
文本
Wolfram Research (2014),HiddenMarkovProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
CMS
Wolfram 语言. 2014. "HiddenMarkovProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
APA
Wolfram 语言. (2014). HiddenMarkovProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html 年