HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
is the generalized hypergeometric function ![]() .
.




HypergeometricPFQ
HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
is the generalized hypergeometric function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
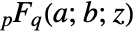 has the series expansion
has the series expansion ![sum_(k=0)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k/k! sum_(k=0)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k/k!](Files/HypergeometricPFQ.en/3.png) , where
, where ![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/HypergeometricPFQ.en/4.png) is the Pochhammer symbol.
is the Pochhammer symbol.- Hypergeometric0F1, Hypergeometric1F1, and Hypergeometric2F1 are special cases of HypergeometricPFQ.
- In many special cases, HypergeometricPFQ is automatically converted to other functions.
- For certain special arguments, HypergeometricPFQ automatically evaluates to exact values.
- HypergeometricPFQ can be evaluated to arbitrary numerical precision.
- For
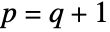 , HypergeometricPFQ[alist,blist,z] has a branch cut discontinuity in the complex
, HypergeometricPFQ[alist,blist,z] has a branch cut discontinuity in the complex 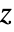 plane running from
plane running from 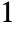 to
to 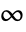 .
. - FullSimplify and FunctionExpand include transformation rules for HypergeometricPFQ.
- HypergeometricPFQ can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (5)
Scope (34)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments and parameters:
Evaluate HypergeometricPFQ efficiently at high precision:
HypergeometricPFQ threads elementwise over lists in its third argument:
HypergeometricPFQ threads elementwise over sparse and structured arrays in its third argument:
HypergeometricPFQ can be used with Interval and CenteredInterval objects:
Compute the elementwise values of an array:
Or compute the matrix HypergeometricPFQ function using MatrixFunction:
Specific Values (4)
For simple parameters, HypergeometricPFQ evaluates to simpler functions:
HypergeometricPFQ evaluates to a polynomial if any of the parameters ak is a non-positive integer:
Visualization (2)
Function Properties (9)
Domain of HypergeometricPFQ:
HypergeometricPFQ is an analytic function of z for specific values:
HypergeometricPFQ is neither non-decreasing nor non-increasing for specific values:
HypergeometricPFQ[{1,1,1},{3,3,3},z] is injective:
HypergeometricPFQ[{1,1,1},{3,3,3},z] is not surjective:
HypergeometricPFQ is neither non-negative nor non-positive:
HypergeometricPFQ[{1,1,2},{3,3},z] has both singularity and discontinuity for z≥1 and at zero:
HypergeometricPFQ is neither convex nor concave:
Differentiation (2)
Integration (3)
Indefinite integral of HypergeometricPFQ:
Definite integral of HypergeometricPFQ:
Series Expansions (4)
Taylor expansion for HypergeometricPFQ:
Plot the first three approximations for ![]() around
around ![]() :
:
General term in the series expansion of HypergeometricPFQ:
Expand HypergeometricPFQ of type ![]() into a series at the branch point
into a series at the branch point ![]() :
:
Expand HypergeometricPFQ into a series around ![]() :
:
Function Representations (4)
HypergeometricPFQ can be represented as a DifferentialRoot:
HypergeometricPFQ can be represented in terms of MeijerG:
TraditionalForm formatting:
Applications (7)
Solve a differential equation of hypergeometric type:
Solve a third-order singular ODE in terms of the HypergeometricPFQ and MeijerG functions:
Verify that the components of the general solution for an ODE are linearly independent:
A formula for solutions to the trinomial equation ![]() :
:
Effective confining potential in random matrix theory for a Gaussian density of states:
Its series expansion at infinity reveals logarithmic growth:
An expression for the surface tension of an electrolyte solution as a function of concentration y:
Onsager–Samaras limiting law for very low concentrations:
Fractional derivative of Sin:
Derivative of order ![]() of Sin:
of Sin:
Plot a smooth transition between the derivative and integral of Sin:
Define the Gram polynomial in terms of HypergeometricPFQ:
Verify a discrete orthogonality relation satisfied by the Gram polynomials:
Use the Gram polynomial to compute the Savitzky–Golay smoothing coefficients:
Compare with the result of SavitzkyGolayMatrix:
Properties & Relations (3)
Integrate frequently returns results containing HypergeometricPFQ:
Sum may return results containing HypergeometricPFQ:
Use FunctionExpand to transform HypergeometricPFQ into less general functions:
Possible Issues (2)
Machine-precision input may be insufficient to get a correct answer:
With exact input, the answer is correct:
Common symbolic parameters in HypergeometricPFQ generically cancel:
However, when there is a negative integer among common elements, HypergeometricPFQ is interpreted as a polynomial:
Tech Notes
Related Guides
Related Links
History
Introduced in 1996 (3.0) | Updated in 1999 (4.0) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1996), HypergeometricPFQ, Wolfram Language function, https://reference.wolfram.com/language/ref/HypergeometricPFQ.html (updated 2022).
CMS
Wolfram Language. 1996. "HypergeometricPFQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HypergeometricPFQ.html.
APA
Wolfram Language. (1996). HypergeometricPFQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricPFQ.html
BibTeX
@misc{reference.wolfram_2025_hypergeometricpfq, author="Wolfram Research", title="{HypergeometricPFQ}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HypergeometricPFQ.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_hypergeometricpfq, organization={Wolfram Research}, title={HypergeometricPFQ}, year={2022}, url={https://reference.wolfram.com/language/ref/HypergeometricPFQ.html}, note=[Accessed: 06-February-2026]}