HypergeometricPFQ
HypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
一般化された超幾何関数![]() である.
である.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
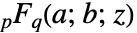 は,級数展開
は,級数展開![sum_(k=0)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k/k! sum_(k=0)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k/k!](Files/HypergeometricPFQ.ja/3.png) を持つ.ただし,
を持つ.ただし,![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/HypergeometricPFQ.ja/4.png) はPochhammer記号である.
はPochhammer記号である.- Hypergeometric0F1,Hypergeometric1F1,Hypergeometric2F1は,HypergeometricPFQの特殊形である.
- 多くの特殊形において,HypergeometricPFQは自動的に他の関数に変換される.
- 特別な引数の場合,HypergeometricPFQは,自動的に厳密値を計算する.
- HypergeometricPFQは任意の数値精度で評価できる.
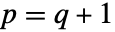 に対し,HypergeometricPFQ[alist,blist,z]は,複素
に対し,HypergeometricPFQ[alist,blist,z]は,複素 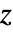 平面上,
平面上,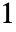 〜
〜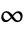 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ.- FullSimplifyとFunctionExpandはHypergeometricPFQの変換規則を含む.
- HypergeometricPFQはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (5)
スコープ (34)
数値評価 (6)
HypergeometricPFQを高精度で効率よく評価する:
HypergeometricPFQはその第3引数のリストに対して要素単位で縫い込まれる:
HypergeometricPFQは第3引数の疎な配列と構造化配列に対して要素単位で縫い込まれる:
HypergeometricPFQはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる:
MatrixFunctionを使って行列のHypergeometricPFQ関数を計算することもできる:
特定の値 (4)
単純なパラメータについては,HypergeometricPFQは評価するとより簡単な関数になる:
HypergeometricPFQは,パラメータ akのいずれかが非正整数である場合,評価すると多項式になる:
可視化 (2)
関数の特性 (9)
HypergeometricPFQは特定の値について z の解析関数である:
HypergeometricPFQは特定の値について非減少でも非増加でもない:
HypergeometricPFQ[{1,1,1},{3,3,3},z]は単射である:
HypergeometricPFQ[{1,1,1},{3,3,3},z]は全射ではない:
HypergeometricPFQは非負でも非正でもない:
HypergeometricPFQ[{1,1,2},{3,3},z]は z≥1および零点に特異点と不連続点の両方を持つ:
HypergeometricPFQは凸でも凹でもない:
積分 (3)
級数展開 (4)
HypergeometricPFQのテイラー(Taylor)展開:
HypergeometricPFQの級数展開における一般項:
タイプ ![]() のHypergeometricPFQを分岐点
のHypergeometricPFQを分岐点 ![]() における級数に展開する:
における級数に展開する:
HypergeometricPFQを ![]() の周りで級数に展開する:
の周りで級数に展開する:
関数表現 (4)
HypergeometricPFQはDifferentialRootとして表現できる:
HypergeometricPFQはMeijerGによって表現できる:
TraditionalFormによる表示:
アプリケーション (7)
三次特異常微分方程式をHypergeometricPFQ関数とMeijerG関数によって解く:
状態のガウス(Gauss)密度についてのランダム行列理論中の有効封圧ポテンシャル:
Sinの分数微分:
Sinの次数![]() の微分:
の微分:
Sinの微分と積分間のスムーズな移行をプロットする:
Gram多項式をHypergeometricPFQによって意定義する:
Gram多項式を使ってSavitzky–Golayの平滑化係数を計算する:
SavitzkyGolayMatrixの結果と比較する:
特性と関係 (3)
IntegrateはしばしばHypergeometricPFQを含む結果を返す:
SumもHypergeometricPFQを含む結果を返すことがある:
FunctionExpandを使ってHypergeometricPFQをそれほど一般的ではない関数に変換する:
考えられる問題 (2)
HypergeometricPFQの共通記号パラメータは,一般に相殺される:
しかし,共通要素に負の整数が含まれるときは,HypergeometricPFQは多項式であると解釈される:
テキスト
Wolfram Research (1996), HypergeometricPFQ, Wolfram言語関数, https://reference.wolfram.com/language/ref/HypergeometricPFQ.html (2022年に更新).
CMS
Wolfram Language. 1996. "HypergeometricPFQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HypergeometricPFQ.html.
APA
Wolfram Language. (1996). HypergeometricPFQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricPFQ.html