グラフ g の頂点と辺の結合行列を与える.
IncidenceMatrix[{vw,…}]
規則 vw を使ってグラフ g を指定する.


IncidenceMatrix
グラフ g の頂点と辺の結合行列を与える.
IncidenceMatrix[{vw,…}]
規則 vw を使ってグラフ g を指定する.
詳細

- IncidenceMatrixは.頂点辺接続行列としても知られている.
- IncidenceMatrixはSparseArrayオブジェクトを返す.これはNormalを使って通常の行列に変換することができる.
- 頂点{v1,…,vn},辺{e1,…,em}である無向グラフについての結合行列は,項 aijが以下で与えられる
 行列である.
行列である. -
0 viは ejと結合していない 1 ej=vivk,ej=vkviまたは ej=vkvi -1 ej=vivk 2 ej=vivi -2 ej=vivi - 頂点 vi はVertexList[g]で返される順序になっており,辺 ej はEdgeList[g]で返される順序になっていると仮定される.
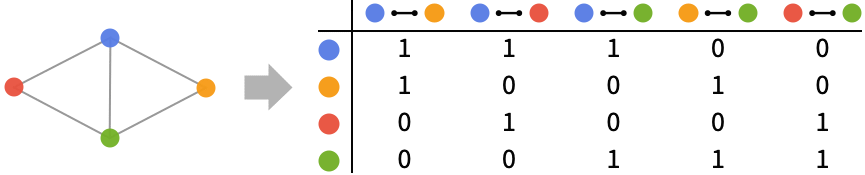
例題
すべて開く すべて閉じるスコープ (5)
IncidenceMatrixは大きいグラフに使うことができる:
MatrixPlotを使って行列を可視化する:
特性と関係 (9)
行と列の順序はVertexListおよびEdgeListの順序に対応する:
VertexIndexおよびEdgeIndexを使って頂点と辺の指標を求める:
DirectedGraphを使って無向グラフの指向結合行列を計算する:
結合行列の次元はVertexCountおよびEdgeCountで与えられる:
IncidenceGraphを使って結合行列からグラフを構築する:
線グラフの隣接行列はそのIncidenceMatrixで計算することができる:
関連するガイド
-
▪
- グラフと行列 ▪
- グラフの構築と表現 ▪
- グラフプログラミング
テキスト
Wolfram Research (2010), IncidenceMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/IncidenceMatrix.html (2015年に更新).
CMS
Wolfram Language. 2010. "IncidenceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/IncidenceMatrix.html.
APA
Wolfram Language. (2010). IncidenceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IncidenceMatrix.html
BibTeX
@misc{reference.wolfram_2025_incidencematrix, author="Wolfram Research", title="{IncidenceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/IncidenceMatrix.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_incidencematrix, organization={Wolfram Research}, title={IncidenceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/IncidenceMatrix.html}, note=[Accessed: 18-February-2026]}