gives the Kirchhoff matrix of the graph g.
KirchhoffMatrix[{vw,…}]
uses rules vw to specify the graph g.


KirchhoffMatrix
gives the Kirchhoff matrix of the graph g.
KirchhoffMatrix[{vw,…}]
uses rules vw to specify the graph g.
Details

- The KirchhoffMatrix is also known as the Laplacian matrix.
- KirchhoffMatrix returns a SparseArray object, which can be converted to an ordinary matrix using Normal.
- The diagonal entries ki,i equal the degree of vi.
- An entry ki,j is -1 if vertex vi is adjacent to vj.
- The vertices vi are assumed to be in the order given by VertexList[g].
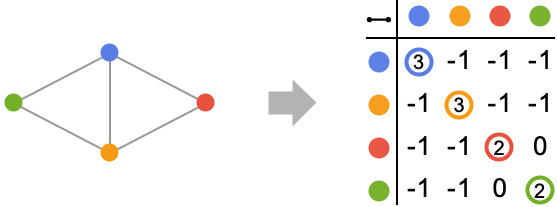
- The Kirchhoff matrix for a graph will have dimensions
 ×
× where
where 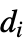 is the number of vertices.
is the number of vertices.
Background & Context
- KirchhoffMatrix returns the Kirchhoff matrix, also known as the Laplacian matrix, admittance matrix, or discrete Laplacian. This is a square matrix with integer elements. For efficiency, KirchhoffMatrix returns the matrix as a sparse array. The (usual) Kirchhoff matrix L is defined as the difference L=D-A of the degree matrix D (the diagonal matrix of graph vertex degrees
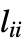 ) and the adjacency matrix A. The diagonal elements
) and the adjacency matrix A. The diagonal elements 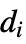 of L are therefore equal to the degree
of L are therefore equal to the degree 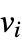 of vertex
of vertex 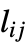 and off-diagonal elements
and off-diagonal elements 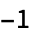 are equal to
are equal to 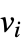 if vertex
if vertex 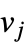 is adjacent to
is adjacent to 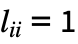 and 0 otherwise.
and 0 otherwise. - For a graph on n vertices, the Kirchhoff matrix has dimensions n×n. For an undirected graph, the Kirchhoff matrix is symmetric.
- The Kirchhoff matrix plays a central role in spectral graph theory, which is the study of graphs based on the eigenvalues of their adjacency or Kirchhoff matrices. It can be used to calculate resistance distances between vertices of a graph, which are defined as the effective resistances between vertices (as when a battery is attached across them) when each graph edge is replaced by a unit resistor. It also appears in the matrix tree theorem, which gives the number of spanning trees of a graph. The second smallest eigenvalue of the Kirchhoff matrix is known as the algebraic connectivity of a graph, and a graph is connected if and only if this eigenvalue is greater than 0. The eigenvector corresponding to the algebraic connectivity of a graph is known as the Fiedler vector and is important in spectral graph partitioning, which is the division of a given graph into smaller components with specific properties based on the eigenvalues of the adjacency or Kirchhoff matrix.
- Note that physicists commonly use the term “Laplacian matrix” instead of “Kirchhoff matrix”. Some physicists and mathematicians also use a version of the matrix with a different normalization, namely that defined by
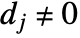 if i=j and
if i=j and 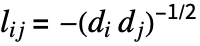 ,
, 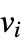 if
if 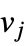 and
and 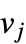 are adjacent, and 0 otherwise. Furthermore, while the term “graph spectrum” generally refers to eigenvalues of a graph adjacency matrix to mathematicians, to physicists it often refers to eigenvalues of the normalized Kirchhoff matrix. Care is therefore needed when encountering these terms in the wild.
are adjacent, and 0 otherwise. Furthermore, while the term “graph spectrum” generally refers to eigenvalues of a graph adjacency matrix to mathematicians, to physicists it often refers to eigenvalues of the normalized Kirchhoff matrix. Care is therefore needed when encountering these terms in the wild. - KirchhoffGraph can be used to construct a graph from a Kirchhoff matrix. The similar functions AdjacencyGraph and IncidenceGraph construct graphs from a given adjacency and incidence matrix, respectively.
Examples
open all close allBasic Examples (2)
Scope (5)
The Kirchhoff matrix of an undirected graph is symmetric:
The Kirchhoff matrix of a directed graph can be unsymmetric:
The Kirchhoff matrix of a non-simple graph and its simple graph is the same:
Use rules to specify the graph:
KirchhoffMatrix works with large graphs:
Use MatrixPlot to visualize the matrix:
Properties & Relations (8)
Rows and columns of the Kirchhoff matrix follow the order given by VertexList:
Use KirchhoffGraph to construct a graph from a Kirchhoff matrix:
The degree of vertices can be found using the diagonal of the Kirchhoff matrix:
The number of rows or columns of the Kirchhoff matrix is equal to the number of vertices:
The off-diagonal entries of a Kirchhoff matrix are ![]() or
or ![]() :
:
For a complete graph, all entries outside the diagonal are ![]() in the Kirchhoff matrix:
in the Kirchhoff matrix:
A complete ![]() -partite graph has
-partite graph has ![]() off-diagonal block entries:
off-diagonal block entries:
In particular, TuranGraph and StarGraph are bipartite:
A path graph will have ![]() or
or ![]() in the diagonal and
in the diagonal and ![]() off-diagonal bands:
off-diagonal bands:
See Also
KirchhoffGraph AdjacencyMatrix IncidenceMatrix WeightedAdjacencyMatrix VertexIndex
Function Repository: KirchhoffTensor
Related Guides
Text
Wolfram Research (2010), KirchhoffMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/KirchhoffMatrix.html (updated 2015).
CMS
Wolfram Language. 2010. "KirchhoffMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/KirchhoffMatrix.html.
APA
Wolfram Language. (2010). KirchhoffMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KirchhoffMatrix.html
BibTeX
@misc{reference.wolfram_2025_kirchhoffmatrix, author="Wolfram Research", title="{KirchhoffMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_kirchhoffmatrix, organization={Wolfram Research}, title={KirchhoffMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}, note=[Accessed: 28-February-2026]}