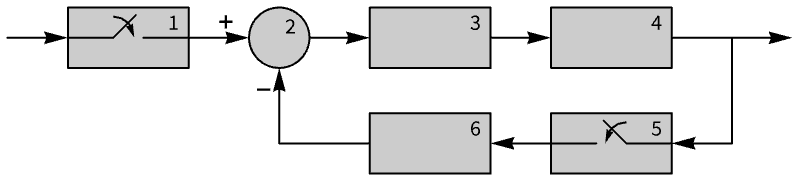
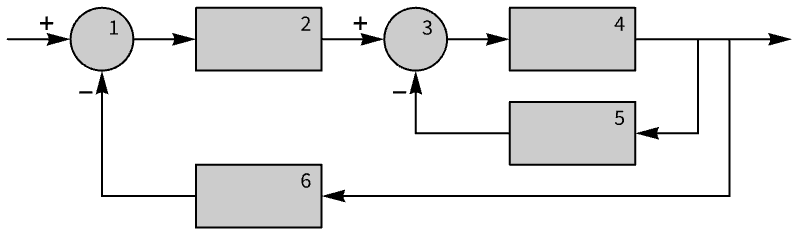
InputOutputResponse
InputOutputResponse[sys,u,tspec]
入力信号 u,一次指定 tspec で入出力モデル sys の応答を与える.
InputOutputResponse[sys,…,"prop"]
特性"prop"の値を与える.
詳細とオプション


- InputOutputResponse は,シミュレーションとしても知られている.
- InputOutputResponseは,しばしば,プラントとコントローラのような系全体のシミュレーションを行い,系の動作を正確に分析し,パフォーマンスを検証し,コントローラ努力を測定するために使われる.
- 結果は,sys のもとになっている方程式を解くことで計算される.一般的には,混合連続または離散系についての,常微分方程式または常差分方程式あるいはそれらの組合せである.
- 混合連続/離散時間系については,結果は連続時間であるが値が区分的であることが多い.
- SystemsConnectionsModelとして表される系については,内部信号もすべて計算することができる.
- 入出力モデルl sys は以下の形を取ることができる.
-
TransferFunctionModel[…] 伝達関数モデル StateSpaceModel[…] 状態空間モデル AffineStateSpaceModel[…] アフィン状態空間モデル NonlinearStateSpaceModel[…] 非線形状態空間モデル DiscreteInputOutputModel[…] 離散入出力モデル SamplerModel[…] サンプル採取器モデル HolderModel[…] ホールダーモデル SystemsConnectionsModel[…] 接続モデル - InputOutputResponse[{sys,ics},…]を使って初期条件 ics が指定できる.
- 入力信号 u は以下の形を取ることができる.
-
{u1[t],…,up[t]} 時間 t の関数としての連続時間信号 ui[t] {{u11,…,u1k},…,{up1,…,upk}} 離散時間信号のシーケンス{ui1,…,uik} {…,ui[t],…,{uj1,…,ujk},…} 連続時間信号と離散時間信号の組合せ - 一次指定 tspec は以下の形を取ることができる.
-
t 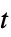 の関数としての記号解を計算する
の関数としての記号解を計算する{t,0,tmax} 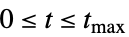 のときの数値解または記号解を計算する
のときの数値解または記号解を計算する - 特性"prop"は以下の形を取ることができる.
-
"Data" InputOutputResponseDataオブジェクト "OutputResponse" リストとしての出力応答 "OutputResponseAssociation" 連想としての出力応答 "PropertyAssociation" 連想としての特性名と値 "PropertyDataset" Datasetとしての特性名と値 "StateResponse" リストとしての状態応答 "StateResponseAssociation" 連想としての状態応答 "SubsystemOutputResponse" リストとしての部分系の出力応答 "SubsystemOutputResponseAssociation" 連想としての部分系の出力応答 {p1,p2,…} 特性 piの値 - InputOutputResponseは,以下の値を取るMethodオプションを取る.
-
"DSolve" DSolve "Integrate" Integrate "Iterate" 積分して解を得る "NDSolve" NDSolve "RecurrenceTable" RecurrenceTable "RSolve" RSolve "Sum" Sum - Method{m,opt1val1,…}のメソッド m は,オプション optiを値 valiに設定して用いられる.
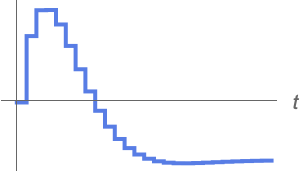
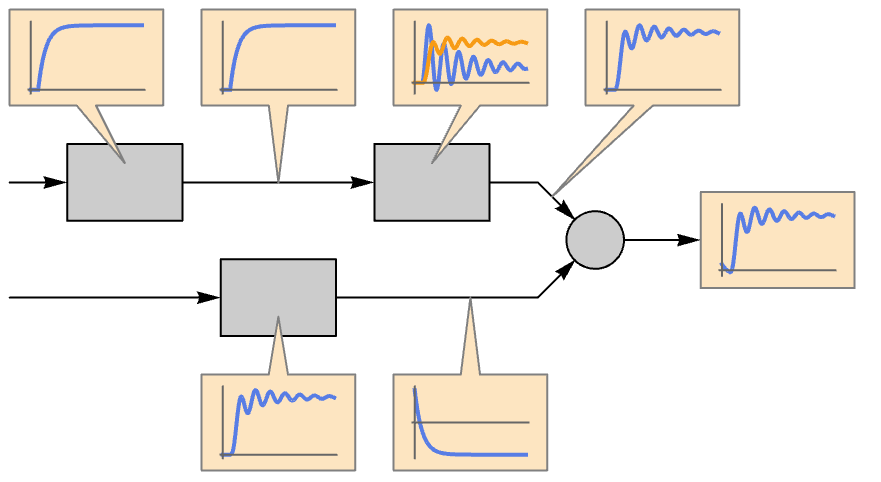
例題
すべて開くすべて閉じる
Wolfram Research (2024), InputOutputResponse, Wolfram言語関数, https://reference.wolfram.com/language/ref/InputOutputResponse.html.
テキスト
Wolfram Research (2024), InputOutputResponse, Wolfram言語関数, https://reference.wolfram.com/language/ref/InputOutputResponse.html.
CMS
Wolfram Language. 2024. "InputOutputResponse." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InputOutputResponse.html.
APA
Wolfram Language. (2024). InputOutputResponse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InputOutputResponse.html