IntegrateChangeVariables

IntegrateChangeVariables[integral,u,trans]

変換 trans を使って integral の変数を新変数 u に変換する．

IntegrateChangeVariables[integral,{u,v,…},trans]

変数を新変数 u, v, …に変更する．

詳細とオプション

  • IntegrateChangeVariablesは置換による積分，u置換，連鎖律の逆としても知られている．
  • 微積分では，しばしば変数の変更を使って適切な代入を行ったり別の座標系で表して問題の対称性を利用したりすることで積分を単純にする．
  • IntegrateChangeVariablesを使って，不定積分，定積分，多重積分，幾何領域上の積分の変数を変更することができる．
  • 変数の変更は変数の変更法則を
  • 区間 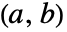あるいは
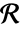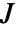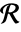  • 領域 上に使って行われる． は 上の 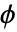の変換のヤコビアンを示す．
  • integral の可能な形はIntegrate:がサポートする形である．
  • Integrate[f[x],x]一変量不定積分
    Integrate[f[x],{x,a,b}]一変量定積分
    Integrate[f[x,y,…],x,y,…]多変量不定積分
    Integrate[f[x,y,…],{x,a,b},{y,c,d},…]多変量定積分
    Integrate[f[x,y,…],{x,y,…}∈reg]領域上の多変量定積分
  • 一変量のIntegrate[…]あるいはInactive[Integrate][…]を使うことができる．integral を評価しないことが大切であるので，安全な方法はInactivate[integral,Integrate]で生成されるInactive[Integrate][…]を使うことであろう．
  • IntegrateChangeVariablesは結果をInactive[Integrate][…]の形で返す．Activateを使って新たな座標で積分を評価する． »
  • 変換 trans には以下の形がある．
  • t==ϕ[x]ϕ[x]を t で置換する
    {u==ϕ[x,y,…],v=ψ[x,y,…],…}ϕ[x,y,…]を u で，ψ[x,y,…]を v で置換する等
    chart1chart2CoordinateChartDataからの名前付き座標系
  • 変換 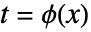は定義領域上で微分可能であると考えられる．
  • 名前付きの座標系を使う際は，{oldsys,metric,dim}{newsys,metric,dim}，{oldsysnewsys,metric,dim}，およびより省略されたさまざまな形式を含む，CoordinateTransformDataが取る任意の形式で変換を入力することができる．
  • 積分における変数およびパラメータの領域についての制限はAssumptionsを使って指定できる．

例題

すべて開くすべて閉じる

例  (4)

不定積分で変数の変更 を適用する：

結果を評価する：

もとの積分の結果と比較する：

定積分で変数の変更 を適用する：

結果を評価する：

もとの積分の結果と比較する：

非アクティブな多重積分を作成する：

多重積分に変数の変更を適用する：

結果を評価する：

もとの積分の結果と比較する：

変数の変更を多重積分の近似に適用する：

結果を評価する：

結果を多重積分のもとの近似と比較する：

スコープ  (21)

不定積分  (5)

変数の変更を 不定積分に適用する：

この変換はもとの変数を新たな変数 によって与えることで行える：

結果を評価してもとの変数に代入し直す：

結果をもとの積分と比較する：

変数の変更 を不定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を不定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 と を不定多重積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

不定積分を直交座標から平面放物線座標に変更する：

定積分  (6)

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更 を定積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

多重積分  (8)

変数の変更を多重積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更を多重積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

多重積分に変数の変更を適用する：

結果を評価する：

上記の結果の数値はNIntegrateが返す結果と一致する：

多重積分に変数の変更を適用する：

結果を評価する：

結果をもとの積分と比較する：

多重積分に変数の変更を適用する：

結果を評価する：

多重積分に変数の変更を適用する：

結果を評価する：

結果をもとの積分と比較する：

多重積分に変数の変更を適用する：

結果を評価する：

多重積分に変数の変更を適用する：

結果を評価する：

結果をもとの積分と比較する：

領域上の積分  (2)

変数の変更 と を領域上の多重積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

変数の変更を領域上の積分に適用する：

結果を評価する：

結果をもとの積分と比較する：

アプリケーション  (4)

アニュラスの面積を計算する：

アニュラスの面積は上記の結果と一致する以下の長方形で表すこともできる：

結果を評価する：

次の領域の面積を計算する：

この領域の面積は次の積分で表される：

この領域は，と という変形で次の正方形に変形される：

結果を評価する：

定積分を計算する．この計算には時間がかかり，部分的にしか評価できない：

極座標系に変換すると，より簡単に計算できる積分が得られる：

上記の結果の数値はNIntegrateが返す結果と同じである：

定積分を計算する．この計算には時間がかかり，部分的にしか評価できない：

極座標系に変換すると，より簡単に計算できる積分が得られる：

上記の結果の数値はNIntegrateが返す結果と同じである：

特性と関係  (2)

結果の頭部は入力の形とは関係なく常に不活性である：

Activateを使って積分を評価する：

IntegrateChangeVariablesはCoordinateChartDataとCoordinateTransformDataの両方からの情報を使う：

前述の例ではマッピングと座標範囲の両方を使用して可能な限り単純な結果を得た：

Wolfram Research (2022), IntegrateChangeVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

テキスト

Wolfram Research (2022), IntegrateChangeVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

CMS

Wolfram Language. 2022. "IntegrateChangeVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

APA

Wolfram Language. (2022). IntegrateChangeVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html

BibTeX

@misc{reference.wolfram_2024_integratechangevariables, author="Wolfram Research", title="{IntegrateChangeVariables}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_integratechangevariables, organization={Wolfram Research}, title={IntegrateChangeVariables}, year={2022}, url={https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html}, note=[Accessed: 17-November-2024 ]}