IntegrateChangeVariables
IntegrateChangeVariables[integral,u,trans]
使用变换 trans 将 integral 中的变量更改为新变量 u.
IntegrateChangeVariables[integral,{u,v,…},trans]
将变量更改为新变量 u、v、….
更多信息和选项


- IntegrateChangeVariables 也称为替代积分、u-替代积分和反向链式法则.
- 微积分中经常通过更改变量简化积分,方法是对变量进行适当的替换或在另一个坐标系中表示,以利用问题的对称性.
- IntegrateChangeVariables 可用于执行不定积分、定积分、多重积分和几何区域积分的变量更改.
- 变量的更改使用变量更改公式
- 在区间
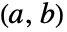 或
或 - 在区域
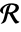 上(其中
上(其中 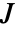 表示变换
表示变换 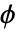 在
在 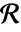 上的雅可比行列式)执行.
上的雅可比行列式)执行. - integral 的可能形式是 Integrate 支持的形式:
-
Integrate[f[x],x] 单变量不定积分 Integrate[f[x],{x,a,b}] 单变量定积分 Integrate[f[x,y,…],x,y,…] 多元不定积分 Integrate[f[x,y,…],{x,a,b},{y,c,d},…] 多元定积分 Integrate[f[x,y,…],{x,y,…}∈reg] 区域上的多元定积分 - 可以使用未运算的 Integrate[…] 或 Inactive[Integrate][…]. 确保 integral 不运算非常重要,因此安全的方法是使用 Inactive[Integrate][…],它可以通过 Inactivate[integral,Integrate] 生成.
- IntegrateChangeVariables 返回形式为 Inactive[Integrate][…] 的结果. 使用 Activate 运算新坐标中的积分. »
- 转换 trans 可以有以下形式:
-
t==ϕ[x] 由 t 替换 ϕ[x] {u==ϕ[x,y,…],v=ψ[x,y,…],…} 由 u 替换 ϕ[x,y,…],由 v 替换 ψ[x,y,…],等等 chart1chart2 来自 CoordinateChartData 的命名坐标系 - 假设变换
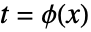 在其定义域上是可微的.
在其定义域上是可微的. - 使用命名坐标系时,可以以 CoordinateTransformData 接受的任何形式输入变换,包括 {oldsys,metric,dim}{newsys,metric,dim}、{oldsysnewsys,metric,dim} 及各种缩写形式.
- 可以使用 Assumptions 指定对积分中变量域和参数的限制.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (21)
应用 (4)
上述结果在数值上与 NIntegrate 返回的结果一致:
上述结果在数值上与 NIntegrate 返回的结果一致:
属性和关系 (2)
使用 Activate 运算积分:
IntegrateChangeVariables 使用来自 CoordinateChartData 和 CoordinateTransformData 的信息:
文本
Wolfram Research (2022),IntegrateChangeVariables,Wolfram 语言函数,https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.
CMS
Wolfram 语言. 2022. "IntegrateChangeVariables." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.
APA
Wolfram 语言. (2022). IntegrateChangeVariables. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html 年