InverseHankelTransform
InverseHankelTransform[expr,s,r]
给出 expr 的 0 阶逆汉克尔 (Hankel) 变换.
InverseHankelTransform[expr,s,r,ν]
给出 expr 的 ν 阶逆汉克尔 (Hankel) 变换.
更多信息和选项

- 函数
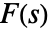 的 ν 阶逆汉克尔 (Hankel) 变换被定义为
的 ν 阶逆汉克尔 (Hankel) 变换被定义为 ![int_0^inftys F(s) TemplateBox[{v, {s, , r}}, BesselJ]ds int_0^inftys F(s) TemplateBox[{v, {s, , r}}, BesselJ]ds](Files/InverseHankelTransform.zh/2.png) .
. - 逆汉克尔变换被定义在
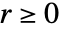 和
和 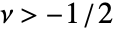 .
. - 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 GenerateConditions False 是否产生与参数的条件有关的结果 Method Automatic 使用什么方法 - 在 TraditionalForm 格式中,用
![TemplateBox[{{F, (, s, )}, s, r, nu}, InverseHankelTransform] TemplateBox[{{F, (, s, )}, s, r, nu}, InverseHankelTransform]](Files/InverseHankelTransform.zh/5.png) 输出 InverseHankelTransform.
输出 InverseHankelTransform.
范例
打开所有单元关闭所有单元范围 (16)
基本用法 (5)
用 TraditionalForm 格式显示:
应用 (3)
平面上径向对称函数的逆傅立叶变换可以被表示为逆汉克尔变换. 用如下定义的函数来验证这种关系:
用 InverseHankelTransform 获取同样的结果:
对方程应用 HankelTransform:
应用 InverseHankelTransform,得到特解:
属性和关系 (7)
用 Asymptotic 计算渐近近似:
InverseHankelTransform 计算的是积分 ![]() :
:
InverseHankelTransform 是 HankelTransform 的逆:
InverseHankelTransform 是自身的逆变换:
InverseHankelTransform 是线性算子:
文本
Wolfram Research (2017),InverseHankelTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/InverseHankelTransform.html.
CMS
Wolfram 语言. 2017. "InverseHankelTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InverseHankelTransform.html.
APA
Wolfram 语言. (2017). InverseHankelTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseHankelTransform.html 年