Wolfram Language & System Documentation Center

InverseHilbertTransform

InverseHilbertTransform[F[t],t,s]

gives the symbolic inverse Hilbert transform of F[t] in the variable t and returns a transform f[s] in the variable s.

InverseHilbertTransform[F[t],t,]

gives the numeric inverse Hilbert transform at the numerical value .

Details

Hilbert transforms are used to solve problems in signal processing, communications and other fields.
The inverse Hilbert transform of a function 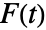is defined to be principal value integral .
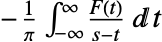InverseHilbertTransform shifts every frequency component of a function by a phase of 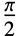radians.
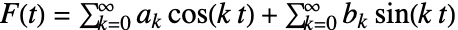
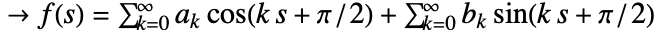
The conjugate function 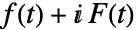is the analytic representation of 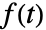and its magnitude is the Envelope:

InverseHilbertTransform is a singular integral transform. Moreover, it is a bounded operator on $L^p(TemplateBox[{}, Reals])$ for .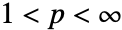
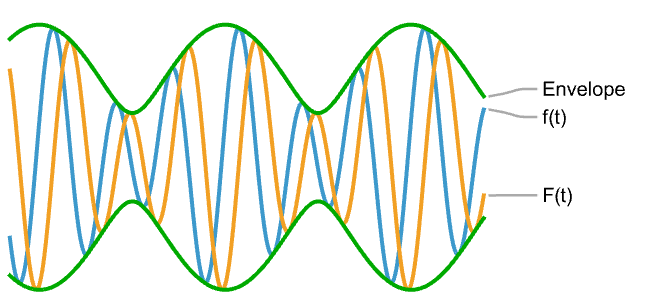
The integral is computed using numerical methods if the third argument, 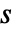, is given a numerical value.
The following options can be given:

AccuracyGoal	Automatic	digits of absolute accuracy sought
Assumptions	$Assumptions	assumptions to make about parameters
GenerateConditions	Automatic	whether to generate answers that involve conditions on parameters
Method	Automatic	method to use
PrecisionGoal	Automatic	digits of precision sought
WorkingPrecision	Automatic	the precision used in internal computations

Examples

open all close all

Basic Examples (4)

Compute the inverse Hilbert transform of a function:

Plot the function and its inverse Hilbert transform:

Inverse Hilbert transform of a simple rational function:

Inverse Hilbert transform of a Cauchy pulse:

Plot both:

Compute the transform at a single point:

Scope (30)

Basic Uses (4)

Inverse Hilbert transform of a function for a symbolic parameter :

Inverse Hilbert transforms of simple trigonometric functions:

Evaluate the inverse Hilbert transform for a numerical value of the parameter :

TraditionalForm formatting:

Elementary Functions (5)

Parabolic pulse:

Plot both:

Square pulse:

Plot both:

Bipolar pulse:

Plot both:

Double triangle pulse:

Plot both:

One-sided rectangular pulse:

Trigonometric Functions (5)

Quotient of trigonometric and linear functions:

Plot both:

Quotient of trigonometric and monomial functions:

Products of cosine functions:

Composition of elementary functions:

Plot the transform:

An inverse trigonometric function:

Powers and Algebraic Functions (5)

Rational functions with linear denominator:

Rational functions with quadratic denominators:

Monomial expression with negative power:

Rational functions with quartic denominators:

Other algebraic functions:

Generalized Functions (2)

DiracDelta of linear arguments:

Derivatives of DiracDelta:

Exponential and Logarithmic Functions (5)

Complex exponential:

Gaussian pulse:

Plot both:

Symmetric exponential:

Plot both:

Composition of a logarithmic function and a polynomial of degree 2:

Plot both:

Quotient of a logarithmic function and a linear monomial:

Plot both:

Special Functions (2)

Legendre polynomials:

Hermite polynomials:

Formal Properties (1)

Inverse Hilbert transform threads itself over equations:

Numerical Evaluation (1)

Calculate the inverse Hilbert transform at a single point:

Alternatively, calculate the Hilbert transform symbolically:

Then evaluate it for the specific value of :

Options (5)

AccuracyGoal (1)

The option AccuracyGoal sets the number of digits of accuracy:

With default settings:

Assumptions (1)

Specify the range of a variable using Assumptions:

GenerateConditions (1)

Use GenerateConditionsTrue to get parameter conditions for when a result is valid:

PrecisionGoal (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision (1)

If WorkingPrecision is specified, the computation is done at that working precision:

With default settings:

Applications (3)

Basic Applications (1)

Consider a sine wave:

InverseHilbertTransform applies a -degree phase shift:

Plot both:

Signals and Systems (2)

The inverse Hilbert filter is defined below. It preserves the magnitude of the signal and phase shifts by for positive frequencies and for negative frequencies: