JacobiDC
JacobiDC[u,m]
gives the Jacobi elliptic function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
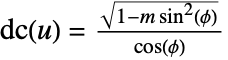 , where
, where 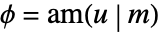 .
. 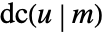 is a doubly periodic function in u with periods
is a doubly periodic function in u with periods 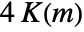 and
and 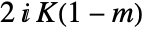 , where
, where 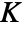 is the elliptic integral EllipticK.
is the elliptic integral EllipticK.- JacobiDC is a meromorphic function in both arguments.
- For certain special arguments, JacobiDC automatically evaluates to exact values.
- JacobiDC can be evaluated to arbitrary numerical precision.
- JacobiDC automatically threads over lists.
Examples
open allclose allBasic Examples (4)
Scope (35)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate JacobiDC efficiently at high precision:
Compute average case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix JacobiDC function using MatrixFunction:
Specific Values (3)
Visualization (3)
Function Properties (8)
JacobiDC is ![]() -periodic along the real axis:
-periodic along the real axis:
JacobiDC is ![]() -periodic along the imaginary axis:
-periodic along the imaginary axis:
JacobiDC is an even function:
![]() is an analytic function of
is an analytic function of ![]() for
for ![]() :
:
It is not, in general, analytic:
It has both singularities and discontinuities for ![]() :
:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
![]() is not injective for any fixed
is not injective for any fixed ![]() :
:
![]() is not surjective for any fixed
is not surjective for any fixed ![]() :
:
JacobiDC is neither non-negative nor non-positive:
JacobiDC is neither convex nor concave:
Differentiation (3)
Series Expansions (3)
Plot the first three approximations for ![]() around
around ![]() :
:
Plot the first three approximations for ![]() around
around ![]() :
:
JacobiDC can be applied to a power series:
Function Identities and Simplifications (4)
Identity involving JacobiNC:
Parity transformations and periodicity relations are automatically applied:
Function Representations (3)
Representation in terms of trigonometric functions and JacobiAmplitude:
Relation to other Jacobi elliptic functions:
TraditionalForm formatting:
Applications (2)
Properties & Relations (2)
Compose with inverse functions:
Use PowerExpand to disregard multivaluedness of the inverse function:
Text
Wolfram Research (1988), JacobiDC, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiDC.html.
CMS
Wolfram Language. 1988. "JacobiDC." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiDC.html.
APA
Wolfram Language. (1988). JacobiDC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiDC.html