Laplacian
詳細

- Laplacianはラプラス(Laplace)・ベルトラミ(Beltrami)演算子としても知られている.ベクトル場に適用されるときは,ベクトルラプラシアンとしても知られている.
- Laplacian[f,x]は
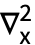 f と入力することができる.記号 ∇ は
f と入力することができる.記号 ∇ は del
del あるいは\[Del]で入力することができる.変数xのリストおよび2は,それぞれ下付き文字および上付き文字として入力される.
あるいは\[Del]で入力することができる.変数xのリストおよび2は,それぞれ下付き文字および上付き文字として入力される. - 空のテンプレート
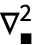 は
は del2
del2 で入力できる.
で入力できる. を使って下付き文字から本体へカーソルを移動することができる.
を使って下付き文字から本体へカーソルを移動することができる. - 指定された変数に明示的に依存しない数量はすべて偏導関数が0であると考えられる.
- Laplacian[f,{x1,x2,…}]は f と同じ次元の結果を与える.
- Laplacian[f,{x1,…,xn},chart]では,f が配列の場合,その次元は{n,…,n}でなければならない.f の成分は chart に関連する正規直交基底にあると解釈される.
- ユークリッド空間の座標グラフについては,Laplacian[f,{x1,…,xn},chart]は f をデカルト座標に変換し,通常のラプラシアンを計算してから再び chart に変換し直すことで計算できる. »
- Laplacianの特性に,chart が正規直交基底で表されている測定値 g で定義されるならLaplacian[g,{x1,…,xn]},chart]はゼロを与えるというものがある. »
- Laplacianの第3引数における座標チャートは,トリプル{coordsys,metric,dim}としてCoordinateChartDataの第1引数におけるのと同じように指定することができる.dim を省略した短縮形を使うこともできる.
- Laplacian[f,VectorSymbol[…]]は,ベクトル記号についてのラプラシアンを計算する. »
- LaplacianはSparseArrayオブジェクトおよび構造配列オブジェクトに使うことができる.
例題
すべて開くすべて閉じる例 (4)
スコープ (6)
Laplacianは任意の階数の配列に適用することができる:
曲線座標系では,一定の成分を持つベクトルでラプラシアンが非零になることがある:
Laplacianは,曲がった空間に使うことができる:
座標ベクトルのラプラシアンはSymbolicZerosArray[{n}]である:
二乗ノルムのラプラシアンはSymbolicIdentityArray[{n}]によって表される:
TensorExpandを使って期待される結果,つまり次元の二倍になるように簡約する:
アプリケーション (3)
特性と関係 (8)
Laplacianは配列の形を保存する:
Gradは正規直交基底を使うので,スカラーのラプラシアンは二重勾配のトレースに等しい:
より高階の配列については,これは二重勾配の最後の2つの指数の縮約である:
ユークリッド座標グラフ c のLaplacianを,デカルト座標に変換して計算してから再びユークリッド座標に変換し直す:
結果はLaplacian[f,{x1,…,xn},c]を直接計算した場合と同じである:
配列のラプラシアンは直交座標においてのみその成分のラプラシアンと等しい:
chart が正規直交基底で表された測定値 g で定義されるなら,Laplacian[g,{x1,…,xn},chart]はゼロである:
三次元平坦空間のベクトル場 ![]() の場合,ラプラシアンは
の場合,ラプラシアンは ![]() に等しい:
に等しい:
次元 ![]() の平坦空間では,ベクトル場のラプラシアンは
の平坦空間では,ベクトル場のラプラシアンは![]() に等しい.
に等しい.![]() では次のようになる:
では次のようになる:
LaplacianはSymmetrizedArrayの対称構造を保存する:
テキスト
Wolfram Research (2012), Laplacian, Wolfram言語関数, https://reference.wolfram.com/language/ref/Laplacian.html (2024年に更新).
CMS
Wolfram Language. 2012. "Laplacian." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Laplacian.html.
APA
Wolfram Language. (2012). Laplacian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Laplacian.html