Laplacian
更多信息

- Laplacian 亦称为 Laplace–Beltrami 算子. 当应用于向量场时,亦称为向量 Laplacian.
- Laplacian[f,x] 可以按
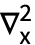 f 输入. 字符 ∇ 可以按
f 输入. 字符 ∇ 可以按  del
del 或者 \[Del] 输入. 变量列表 x 和 2 分别按下标和上标输入.
或者 \[Del] 输入. 变量列表 x 和 2 分别按下标和上标输入. - 可用
 del2
del2 输入空模板
输入空模板 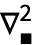 ,通过
,通过  将光标从下标移到主体.
将光标从下标移到主体. - 所有不显式依赖变量的量的偏导数被视为零.
- Laplacian[f,{x1,x2,…}] 给出与 f 具有相同维度的结果.
- 在 Laplacian[f,{x1,…,xn},chart] 中,如果 f 是一个数组,它的维度必须是 {n,…,n}. f 的分量被解释为位于与 chart 相关联的正交规范基中.
- 对于欧几里得空间上的坐标系,可通过将 f 转换至直角坐标系来计算 Laplacian[f,{x1,…,xn},chart],算出拉普拉斯算子后再转换回 chart. »
- Laplacian 的一个属性是如果 chart 是用度规 g 定义的,以正交形式表示,则 Laplacian[g,{x1,…,xn]},chart] 给出零. »
- 可用三元组 {coordsys,metric, dim}(与 CoordinateChartData 的第一个参数相同的方式)指定 Laplacian 的第三个参数中的坐标系. 可以使用忽略了 dim 的简短形式.
- Laplacian[f,VectorSymbol[…]] 计算矢量符号的拉普拉斯算子. »
- Laplacian 适用于 SparseArray 和结构化数组对象.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (6)
将 Laplacian 应用于任意阶数的数组:
在曲线坐标系中,含有常数分量的矢量可能有非零 Laplacian:
Laplacian 作用于弯曲空间:
坐标向量的拉普拉斯算子为 SymbolicZerosArray[{n}]:
平方范数的拉普拉斯算子表示为 SymbolicIdentityArray[{n}]:
使用 TensorExpand 简化为预期结果,即维度的两倍:
应用 (3)
属性和关系 (8)
Laplacian 保留了数组的形状:
由于 Grad 返回标准正交基表示的结果,一个标量的拉普拉斯算子等于双梯度的迹:
通过转换为直角坐标然后再转换回来,计算欧几里得坐标系 c 中的 Laplacian:
与直接计算 Laplacian[f,{x1,…,xn},c] 的结果一样:
一个数组的拉普拉斯算子只在笛卡尔坐标中等于它的分量的拉普拉斯算子:
如果 chart 是用度规 g 定义的,以正交形式表示,则 Laplacian[g,{x1,…,xn},chart] 给出零:
在维度为 ![]() 的平面空间内,向量场的拉普拉斯算子等于
的平面空间内,向量场的拉普拉斯算子等于 ![]() . 对于
. 对于 ![]() :
:
Laplacian 可保留 SymmetrizedArray 对象的对称结构:
文本
Wolfram Research (2012),Laplacian,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Laplacian.html (更新于 2024 年).
CMS
Wolfram 语言. 2012. "Laplacian." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Laplacian.html.
APA
Wolfram 语言. (2012). Laplacian. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Laplacian.html 年