Limit

Limit[f,xx^*]

gives the limit _xx^*f(x).

Limit[f,{x₁,…,x_n}]

gives the nested limit ⋯ f (x₁,…,x_n).

Limit[f,{x₁,…,x_n}{,…,}]

gives the multivariate limit f (x₁,…,x_n).

Details and Options

Limit is also known as function limit, directed limit, iterated limit, nested limit and multivariate limit.
Limit computes the limiting value f^* of a function f as its variables x or x_i get arbitrarily close to their limiting point x^* or .
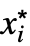By using the character , entered as lim or \[Limit], with underscripts or subscripts, limits can be entered as follows:
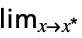f limit in the default direction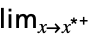

f limit from above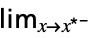

f limit from below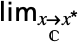

f limit in the complex plane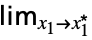

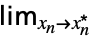…f Limit[f,{x₁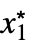,…,x_n}]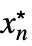
For a finite limit point x^* and {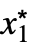,…,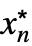} and finite limit value f^*:
Limit[f,xx^*]f^* for every 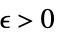there is 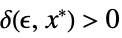such that $0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(epsilon,x^*)$ implies $TemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon$

Limit[f,{x₁,…,x_n}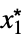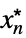{,…,}]f^* for every 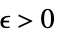there is 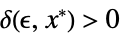such that $0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)$ implies $TemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon$

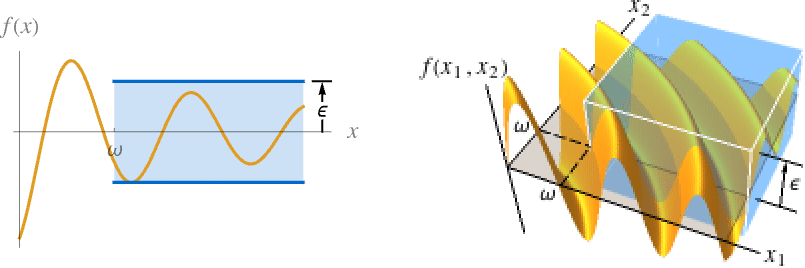
For an infinite limit point and finite limit value f^*:
Limit[f,x∞]f^* for every 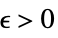there is 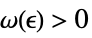such that 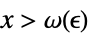implies $TemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon$

Limit[f,{x₁,…,x_n}{∞,…,∞}]f^* for every 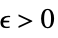there is 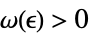such that 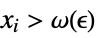implies $TemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon$

Limit returns Indeterminate when it can prove the limit does not exist. MinLimit and MaxLimit can frequently be used to compute the minimum and maximum limit of a function if its limit does not exist.
Limit returns unevaluated or an Interval when no limit can be found. If an Interval is returned, there are no guarantees that this is the smallest possible interval.
The following options can be given:

Assumptions	$Assumptions	assumptions on parameters
Direction	Reals	directions to approach the limit point
GenerateConditions	Automatic	whether to generate conditions on parameters
Method	Automatic	method to use
PerformanceGoal	"Quality"	aspects of performance to optimize

Possible settings for Direction include:

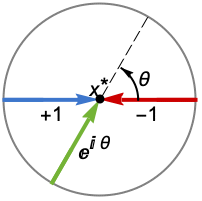
	Reals or "TwoSided"	from both real directions
	"FromAbove" or -1	from above or larger values
	"FromBelow" or +1	from below or smaller values
	Complexes	from all complex directions
	Exp[ θ]	in the direction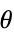
	{dir₁,…,dir_n}	use direction dir_i for variable x_i independently

DirectionExp[ θ] at x^* indicates the direction tangent of a curve approaching the limit point x^*.

Possible settings for GenerateConditions include:
Automatic non-generic conditions only

True all conditions

False no conditions

None return unevaluated if conditions are needed
Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, Limit typically solves more problems or produces simpler results, but it potentially uses more time and memory.

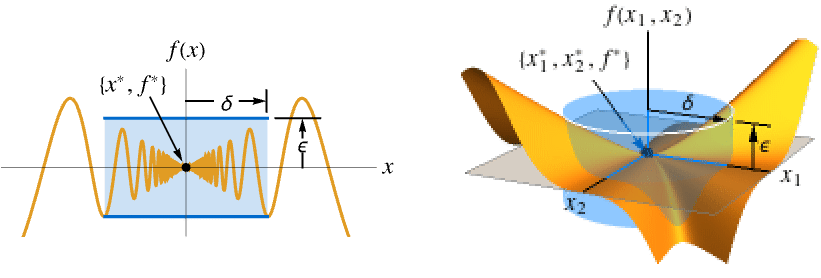
Examples

open allclose all

Basic Examples (3)

Limit at a point of discontinuity:

Limit at infinity:

Limit from above:

Limit from below:

The two-sided limit does not exist:

Scope (35)

Basic Uses (5)

Find the limit at a point:

Find the limit at a symbolic point:

Find the limit at -Infinity:

The nested limit as first and then :

The nested limit as and then :

Compute the multivariate limit as :

Typeset Limits (4)

Use lim to enter the  character, and to create an underscript:

Take a limit from above or below by using a superscript or on the limit point:

After typing zero, use to create a superscript:

To specify a direction of Reals or Complexes, enter the domain as an underscript on the  character:

Enter the rule as ->, use to create an underscript, and type reals to enter :

TraditionalForm formatting:

Elementary Functions (6)

Polynomial and rational functions:

Algebraic functions:

Trigonometric functions:

A trigonometric function with a vertical asymptote:

A wildly oscillatory function with no limit at the origin:

Exponential functions:

Logarithmic functions:

Functions like Sqrt and Log have a two-sided limit along the negative reals:

If approached from above in the complex plane, the same limit value is reached:

However, approaching from below in the complex plane produces a different limit value:

This is due to branch cut where the imaginary part reverses sign as the axis is crossed:

The limit in the complex plane does not exist:

Elementary Functions at Infinity (4)

Limits of algebraic functions at ±Infinity:

Limits of trigonometric functions at ±Infinity:

Limits of exponential and logarithmic functions at infinity:

Compute nested exponential-logarithmic limits:

Piecewise Functions (5)

A discontinuous piecewise function:

A left-continuous piecewise function:

UnitStep is effectively a right-continuous piecewise function:

RealSign is effectively a discontinuous piecewise function:

Find the limit of Floor as x approaches from larger numbers:

Find the limit of Floor as x approaches from smaller numbers:

Special Functions (4)

Limits involving Gamma:

Limits involving Bessel-type functions:

Limits involving exponential integrals:

At every non-positive even integer, Gamma approaches from the left and from the right:

The signs are reversed at the negative odd integers:

Nested Limits (3)

Compute the nested limit as first and then :

The same result is obtained by computing two Limit expressions:

Computing the limit as first and then yields a different answer:

This is again equivalent to two nested limits:

The nested limit as first and then is :

Consider the function for two variables at the origin:

The iterated limit as and then is :

Since the value of the limit depends on the order, the bivariate limit does not exist:

Visualize the function and the values along the two axes computed previously:

Multivariate Limits (4)

Compute the bivariate limit of a function as :

The limit value is if for all , there is a where implies :

For this function, the value will suffice:

The function lies in between the two cones with slope :

Find the limit of a multivariate function:

Various iterated limits exist:

Approaching the origin along the curve yields a third result:

The true two-dimensional limit of the function does not exist:

Visualize the limit near the origin:

Find the limit of a bivariate function at the origin:

The true two-dimensional limit at the origin is zero:

Re-express the function in terms of polar coordinates:

The polar expression is bounded, and the limit as is:

Compute the limit of a trivariate function:

The limit at the origin does not exist:

Limits in the and planes do exist:

But the limit in the plane is direction dependent:

Visualize the function:

Options (13)

Assumptions (2)

Specify conditions on parameters using Assumptions:

Different assumptions can produce different results:

Parameter‐dependent limit:

Direction (5)

Limit from below:

Equivalently:

Limit from above:

Equivalently:

Limits at piecewise discontinuities:

Limits at a simple pole:

Limits at a branch cut:

Compute the bivariate limit approach from different quadrants:

Approaching the origin from the first quadrant:

Equivalently:

Approaching the origin from the second quadrant:

Approaching the origin from the left half-plane:

Approaching the origin from the bottom half-plane:

Visualize the function:

GenerateConditions (3)

Return a result without stating conditions:

This result is only valid if n>0:

Return unevaluated if the results depend on the value of parameters:

By default, conditions are generated that return a unique result:

By default, conditions are not generated if only special values invalidate the result:

With GenerateConditions->True, even these non-generic conditions are reported:

Method (2)

Use Method{"AllowIndeterminateOutput"False} to avoid Indeterminate results:

For oscillatory functions, bounds will be returned as Interval objects:

Use Method{"AllowIntervalOutput"False} to avoid Interval object results:

PerformanceGoal (1)

Use PerformanceGoal to avoid potentially expensive computations:

The default setting uses all available techniques to try to produce a result:

Applications (23)

Geometry of Limits (5)

The limit of the function as is :

This means that for values of close to , has a value close to :

Visualize the function:

The limit makes no statement about the value of at , which in this case is indeterminate:

The function does not have a limit as approaches :

The function has the limit zero:

In increasingly small regions around , continually bounces between , but gets increasingly flat:

The following rational function has a finite limit as :

Compute the that ensures that whenever :

The complicated result can be simplified by focusing on in the range between 0 and 2:

The plot of always "leaves" the rectangle of height and width centered through the sides, not the top or bottom:

Find vertical and horizontal asymptotes of a rational function:

Compute where the denominator is zero:

Verify that the function approaches at the computed values:

Compute the limit value at :

Visualize the function and its asymptotes:

Find the non-vertical, linear asymptote of a function:

Slope of the asymptote:

Compute the asymptote's vertical intercept:

Visualize the function and its asymptote:

Discontinuities (5)

Classify the continuity or discontinuity of f at the origin:

It is not defined at 0, so it cannot be continuous:

Moreover, the limit as x0 does not exist:

However, the limit from below exists:

The limit from above also exists, but has a different value:

Therefore, f has a jump discontinuity at 0:

Classify the continuity or discontinuity of f at the origin:

The function is defined:

The two-sided limit exists but does not equal the function value, so this is a removable discontinuity:

Find and classify the discontinuities of a piecewise function:

The function is not defined at zero so it cannot be continuous there:

The function tends to Infinity (on both sides), so this is an infinite discontinuity:

Next find where the limit does not equal the function:

The limit does exist at x==3, so this is a removable discontinuity:

The function is discontinuous at every multiple of :

For example, at the origin it gives rise to the indeterminate form :

At every even multiple of , the two-sided limit of exists:

This is also true at the odd multiples of , with a different limit:

However, at the half-integer multiples of , the two sided limit does not exist:

The function agrees with where both are defined, but it is also continuous at multiples of :

Show that is continuous at the origin:

Visualize and :

Determine whether the following function is continuous at the origin, and whether limits along rays exist:

The bivariate limit does not exist, so the function is not continuous:

The limit in the left half-plane exists and is zero, so any ray approaching from there has the same limit:

Approaching along the line with gives a result in terms of the slope:

Visualize the four rays with slope :

Derivatives (5)

Compute the derivative of using the definition of derivative:

First compute the difference quotient:

The derivative is the limit as of the difference quotient:

Compute the derivative of at :

The limit of the difference quotient does not exist, so is not differentiable at the origin:

Note that the left and right limits of the difference quotient exist but are unequal:

In this case, the left and right derivatives equal the limits of from the left and right:

Visualize and its derivative; the former has a "kink" at zero, the latter a jump discontinuity:

Determine the differentiability of at :

The limit of the difference quotient exists, so is differentiable and :

Note that the limit as of does not exist, so is discontinuous:

Determine the differentiability of at the point :

The partial derivative with respect to x exists:

As does the one with respect to y:

However, the linearization condition $lim_(r->r_0)(TemplateBox[{{{f, (, {x, ,, y}, )}, -, {f, (, {{x, _, 0}, ,, {y, _, 0}}, )}, -, {{p, (, {{x, _, 0}, ,, {y, _, 0}}, )}, ., {(, {r, -, {r, _, 0}}, )}}}}, RealAbs])/(TemplateBox[{{r, -, {r, _, 0}}}, Norm])=0$ fails, so is not differentiable:

Visualize the function:

Note that the partial derivatives of exist everywhere:

But they are discontinuous at the point :

The derivative is defined as the limit of the difference quotient:

The second derivative can be computed by taking the limit of the second-order difference quotient:

Directly compute the mixed partial derivative by taking a limit:

Mathematical Constants and Expressions (4)

Compute as a limit at Infinity:

The complementary limit at the origin:

Compute as a limit of Gamma functions:

Compute EulerGamma as a limit involving the Zeta function:

Compute EulerGamma as a limit of exponential integrals:

Other Applications (4)

A function is said to be "little-o of " at , written , if $lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=0$ :

Similarly, is said to be "little-omega of ", written , if $lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=infty$ :

If , then :

It is possible for two functions to share neither relationship:

Moreover, neither relationship even holds between a function and itself:

Hence, and define partial orders on the functions:

if goes to zero faster than :

denotes the opposite relationship:

Note that the two lists are not exactly reversed, because and are incomparable:

From Taylor's theorem, if has continuous derivatives around , then :

This is the fifth-order Taylor polynomial at :

The definition of is that $lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=0$ :

Verify that :

In special relativity, the kinetic energy of a particle of mass and speed is given by:

The classical formula for kinetic energy is:

In the limit that the speed approaches zero, these two formulas agree:

Improper integrals:

Properties & Relations (14)

Multiplicative constants can be moved outside a limit:

If f and g have finite limits, Limit is distributive over their sum:

If f and g have finite limits, Limit is distributive over their product:

Powers can be moved outside a limit:

Function composition and sequence limit operations can be interchanged for continuous functions:

This need not hold for discontinuous functions:

The "squeezing" or "sandwich" theorem:

This function is bounded by :

The limit of the bounding functions is zero, which proves the original limit was zero:

The squeezing theorem for limits at infinity:

This function is bounded by on the positive real axis:

The limit of the bounding functions is zero, which proves the original limit was zero:

Assumptions applies to parameters in the limit expression:

Direction places conditions on the limit variable:

Derivatives are defined in terms of limits:

The limit of a ratio can often be computed using L'Hôpital's rule:

Computing the ratio directly gives an indeterminate form 0/0:

The limit of the ratio equals the limit of the ratio of the derivatives:

In this case, f' and g' are continuous and can be computed via evaluation:

If Limit exists, then so does DiscreteLimit, and they have the same value:

The converse need not hold:

If Limit exists, then so does MaxLimit, and it has the same value:

If Limit exists, then so does MinLimit, and it has the same value:

At each point of the domain, the limit of a continuous function is equal to its value:

Use FunctionContinuous to test whether a function is continuous:

Possible Issues (1)

Limit may return an incorrect answer for an inexact input:

The result is correct when an exact input is used:

Numerical cancellations are behind the incorrect result:

Interactive Examples (1)

In a sector bounded by a diameter and perpendicular chord, find the fraction occupied by the triangle:

If the disk has radius r, the area of the light blue shaded right triangle is:

Similarly, the total shaded area is the area of the whole sector minus the area of the white right triangle:

Compute the limit as ϕ approaches 0:

Neat Examples (2)

Differentiation by integration:

Visualize a set of limits:

Top

	f	limit in the default direction
	f	limit from above
	f	limit from below
	f	limit in the complex plane
	…f	Limit[f,{x₁,…,x_n}]

	Limit[f,xx^]f^	for every there is such that $0<TemplateBox[{{x, -, {x, ^, }}}, Abs]<delta(epsilon,x^)$ implies $TemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon$
	Limit[f,{x₁,…,x_n}{,…,}]f^*	for every there is such that $0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, }}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, }}}, }}}, Norm]<delta(epsilon,x^)$ implies $TemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, }}}, Abs]<epsilon$

	Limit[f,x∞]f^*	for every there is such that implies $TemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon$
	Limit[f,{x₁,…,x_n}{∞,…,∞}]f^*	for every there is such that implies $TemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon$

	Automatic	non-generic conditions only
	True	all conditions
	False	no conditions
	None	return unevaluated if conditions are needed

Limit

Details and Options

Examples

Basic Examples (3)

Scope (35)

Basic Uses (5)

Typeset Limits (4)

Elementary Functions (6)

Elementary Functions at Infinity (4)

Piecewise Functions (5)

Special Functions (4)

Nested Limits (3)

Multivariate Limits (4)

Options (13)

Assumptions (2)

Direction (5)

GenerateConditions (3)

Method (2)

PerformanceGoal (1)

Applications (23)

Geometry of Limits (5)

Discontinuities (5)

Derivatives (5)

Mathematical Constants and Expressions (4)

Other Applications (4)

Properties & Relations (14)

Possible Issues (1)

Interactive Examples (1)

Neat Examples (2)

See Also

Tech Notes

Related Guides

History

Text

CMS

APA

BibTeX

BibLaTeX