Limit

Limit[f,xx*]

極限xx*f(x)を与える．

Limit[f,{x1,…,xn}]

ネストした極限⋯ f (x1,…,xn)を与える．

Limit[f,{x1,…,xn}{,…,}]

多変量の極限f (x1,…,xn)を与える．

詳細とオプション

  • Limitは，関数極限，有向極限，反復極限，ネスト極限，多変量極限としても知られている．
  • Limitは，変数 x または xiが極限点 x*または 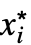に任意に近付くときの，関数 f の極限値 f*を計算する．
  • 文字 を使って，limまたは \[Limit]として，上付き文字または下付き文字とともに，以下のように極限を入力することができる．
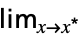  • fデフォルト方向の極限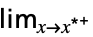
    f上からの極限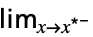
    f下からの極限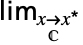
    f複素平面上の極限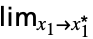
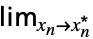    …fLimit[f,{x1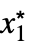,…,xn}]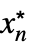
  • 有限極限点 x*および{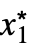,…,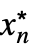}と有限極限値 f*
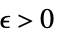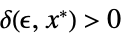  • Limit[f,xx*]f*すべての について，0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(epsilon,x^*) がTemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
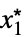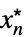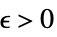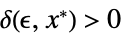    Limit[f,{x1,…,xn}{,…,}]f*すべての について，0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)がTemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
  • 無限極限点と有限極限値 f*について
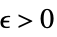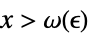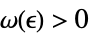  • Limit[f,x∞]f*すべての について，が TemplateBox[{{{f, (, x, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
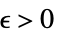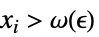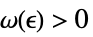    Limit[f,{x1,…,xn}{∞,…,∞}]f*すべての について，がTemplateBox[{{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}, -, {f, ^, *}}}, Abs]<epsilon を暗示するような が存在する
  • Limitは，極限が存在しないと証明できるときはIndeterminateを返す．関数に極限が存在しない場合の最大極限と最小極限の計算にMinLimitとMaxLimitが頻繁に使われる．
  • Limitは，極限が求まらないときは，未評価で返されたりIntervalを返したりする．Intervalが返されたときは，それが可能な最小の区間である保証はない．
  • 使用可能なオプション
  • Assumptions $Assumptionsパラメータについての仮定
    Direction Reals極限点に近付く方向
    GenerateConditions Automaticパラメータについての条件を生成するかどうか
    Method Automatic使用するメソッド
    PerformanceGoal "Quality"パフォーマンスのどの面について最適化するか
  • Directionの可能な設定
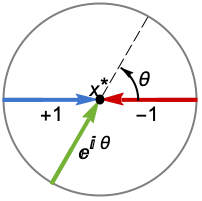
  • Reals または "TwoSided"両方の実方向から
    "FromAbove" または -1上またはより大きい値から
    "FromBelow" または +1下またはより小さい値から
    Complexesすべての複素方向から
    Exp[ θ] 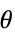方向
    {dir1,…,dirn}変数 xiに独立に diri方向を使う
  • x*におけるDirectionExp[ θ]は，極限点 x*に近付く曲線の接線の方向を示している．
  • GenerateConditionsの可能な設定
  • Automatic一般的ではない条件のみ
    Trueすべての条件
    False条件なし
    None条件が必要なときは未評価で返す
  • PerformanceGoalの可能な設定には，$PerformanceGoal，"Quality"，"Speed"がある．"Quality"と設定すると，Limitでより多くの問題が解かれたり単純な結果が与えられたりするが，時間とメモリ消費は大きくなる可能性がある．

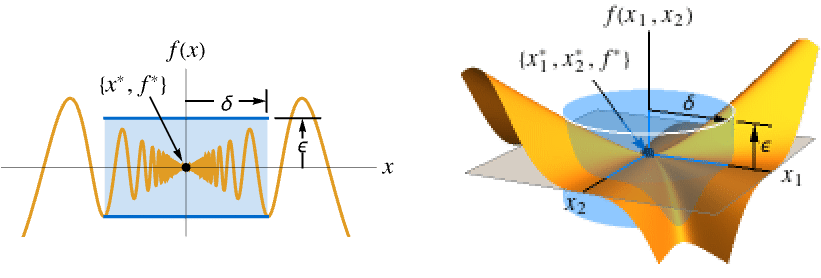
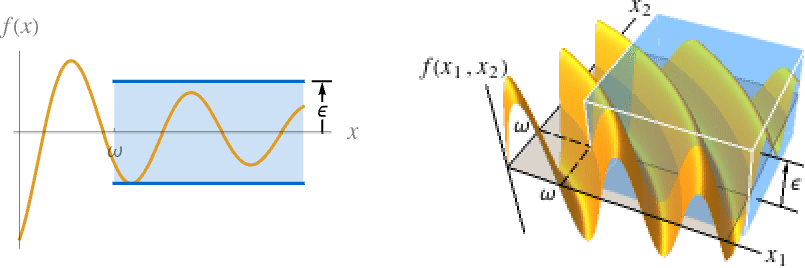
例題

すべて開くすべて閉じる

例  (3)

不連続点における極限：

無限大における極限：

上からの極限：

下からの極限：

両側極限は存在しない：

スコープ  (35)

基本的な用法  (5)

ある点における極限を求める：

記号点における極限を求める：

-Infinityにおける極限を求める：

まず ，次に のネストした極限：

まず ，次に のネストした極限：

のときの多変量極限を求める：

極限のタイプセット  (4)

limで 記号を入力し，で下付き文字を作る：

下付き文字 または を極限点に使って上または下からの極限を取る：

0を入力した後で，を使って上付き文字を作る：

RealsまたはComplexesの方向の指定は，定義域を記号の下付き文字として入力する：

規則を->で入力し，を使って下付き文字を作り，realsを使ってを入力する：

TraditionalFormによる表示：

初等関数  (6)

多項式関数と有理関数：

代数関数：

三角関数：

垂直漸近線のある三角関数：

原点に極限がない，大きく振動する関数：

指数関数：

対数関数：

SqrtやLogのような関数には，負の実数に沿って両側極限がある：

複素平面上で上から近付くと，同じ極限値に達する：

しかし，複素平面上で下から近付くと異なる極限値になる：

これは，軸の交差で虚部の符号が変わる分枝切断線のためである：

複素平面上の極限は存在しない：

無限大における初等関数  (4)

±Infinityにおける代数関数の極限：

±Infinityにおける三角関数の極限：

無限大における指数関数と対数関数の極限：

ネストした指数対数極限を計算する：

区分関数  (5)

不連続区分関数：

左連続区分関数：

UnitStepは，事実上，右連続区分関数である：

RealSignは，事実上，不連続区分関数である：

より大きい数からx が近付いてくるときのFloorの極限を求める：

より小さい数からx が近付いてくるときのFloorの極限を求める：

特殊関数  (4)

Gammaを含む極限：

ベッセル(Bessel)型の関数を含む極限：

指数積分を含む極限：

非正の偶数ごとにGammaは左から に近付き，右から に近付く：

負の奇数のところで符号が変わる：

ネストした極限  (3)

まず について，次に について，ネストした極限を計算する：

2つのLimit式を計算しても同じ結果が得られる：

まず について，次に について極限を計算すると，違う答になる：

これもまた，ネストした2つの極限に等しい：

まず について，次に についてのネストした極限はになる：

まず について，次に についてのネストした極限は になる：

原点における2変数の関数について考察する：

まず ，次に の反復極限はである：

まず ，次に の反復極限はである：

極限の値は順序に依存するので，2変量の極限は存在しない：

関数と値を計算済みの2本の軸に沿って可視化する：

多変量極限  (4)

となるときの関数の2変量極限を計算する：

すべての について （は epsilon>TemplateBox[{{{f, (, {x, ,, y}, )}, -, L}}, Abs]を含意）が存在するなら極限値は である：

値 はこの関数を満足する：

この関数は傾斜がの2つの円錐の間にある：

多変量関数の極限を求める：

さまざまな反復極限が存在する：

曲線 に沿って原点に近付くと3番目の結果が与えられる：

関数の真の二次元極限は存在しない：

原点付近の極限を可視化する：

2変量関数の原点における極限を求める：

原点における真の二次元極限は0である：

関数を極座標で再表現する：

極表現は有界であり，のときの極限は以下のようになる：

3変量関数の極限を計算する：

原点には極限は存在しない：

しかし， 平面と 平面には極限が存在する：

平面における極限は方向に依存する：

関数を可視化する：

オプション  (13)

Assumptions  (2)

Assumptionsを使ってパラメータについての条件を指定する：

仮定によって結果が異なる：

パラメータに依存する極限：

Direction  (5)

下からの極限：

同様に：

上からの極限：

同様に：

区分不連続点における極限：

単純極における極限：

分枝切断線における極限：

異なる象限から近付く2変量の極限を計算する：

第1象限から原点に近付く：

同様に：

第2象限から原点に近付く：

左半平面から原点に近付く：

下半平面から原点に近付く：

関数を可視化する：

GenerateConditions  (3)

結果を初期条件なしで返す：

結果は n>0のときにのみ有効である：

結果がパラメータの値に依存する場合は，未評価で返される：

デフォルトで，一意的な結果を返す条件が生成される：

デフォルトで，特殊な値が結果を無効にする場合にのみ条件が生成されなくなる：

GenerateConditions->Trueとすると，一般的ではない条件も報告される：

Method  (2)

Method{"AllowIndeterminateOutput"False}を使ってIndeterminateな結果を避ける：

振動関数については，境界がIntervalオブジェクトとして返される：

Method{"AllowIntervalOutput"False}を使ってIntervalオブジェクトの結果を避ける：

PerformanceGoal  (1)

PerformanceGoalを使って，高くつく可能性がある計算を回避する：

デフォルト設定では，使用可能なすべてのテクニックを使って結果を出そうとする：

アプリケーション  (23)

極限の幾何学  (5)

のときの関数 の極限はである：

これは， の値がに近いとき， の値はに近いことを意味している：

関数を可視化する：

極限はにおける の値（この場合は不定）について何も陳述しない：

関数 は が に近付くときに極限を持たない：

関数 の極限は0である：

の周りの徐々に狭まる領域では， は連続的に間で振動するが， は徐々に平らになる：

次の有理関数は のとき有限極限を持つ：

0<TemplateBox[{{x, -, 1}}, RealAbs]<delta のとき常にTemplateBox[{{{r, (, x, )}, -, 2}}, RealAbs]<epsilon となることを保証する を計算する：

0から2の範囲の に焦点を当てることで複雑な結果を簡約することができる：

のプロットは，常に，上下ではない辺を通るを中心とした高さ で幅 の長方形を「残す」：

有理関数の垂直および水平漸近線を求める：

分母が0になるところを計算する：

関数が計算された値でに近付くことを可視化する：

における極限値を計算する：

関数とその漸近線を可視化する：

関数の非垂直線形漸近線を求める：

漸近線の傾き：

漸近線の垂直切片を計算する：

関数とその漸近線を可視化する：

不連続性  (5)

原点における f の連続性あるいは不連続性を分類する：

0においては定義されないので，連続ではあり得ない：

さらに，x0のときの極限は存在しない：

しかし，下からの極限は存在する：

上からの極限も存在するが，値が異なる：

したがって，f は0で跳躍不連続性を持つ：

原点における f の連続性あるいは不連続性を分類する：

関数は以下のように定義される：

両側極限が存在するが，関数の値とは等しくないので，これは除去可能な不連続性である：

区分関数の不連続性を求め，分類する：

この関数は0で定義されないので，この点では連続ではない：

この関数は（両側で）Infinityに近付くので，無限不連続である：

次に，極限が関数と等しくならないところを求める：

極限が x==3に存在するので，これは除去可能な不連続性である：

関数 はすべての の倍数において不連続である：

例えば，原点ではから不定への上昇が見られる：

のすべての偶数倍において， の両側極限が存在する：

このことは，別の極限ではあるが， の奇数倍においても真である：

しかし， の半整数倍には両側極限は存在しない：

関数 は，両側が定義されている場合は と一致し， の倍数のところでが連続的である：

が原点で連続的であることを示す：

と を可視化する：

次の関数が原点で連続的かどうか，また半直線に沿った極限が存在するかどうかを見る：

2変量の極限が存在しないので，この関数は連続的ではない：

極限は左半平面に存在し，0であるので，そこから近付く半直線はすべて同じ極限を持つ：

直線 ()に沿って近付くと，傾きについての結果が与えられる：

傾きの4本の半直線を可視化する：

導関数  (5)

導関数の定義を使って の導関数を計算する：

まず，差分商を求める：

導関数は のときの差分商の極限である：

における の導関数を計算する：

差分商の極限は存在しないので， は原点で微分不可能である：

左右の極限に差分商が存在するが，両者は等しくない点に注意のこと：

この場合，左右の導関数は左右からの の極限に等しい：

とその導関数を可視化する．前者は0に「ねじれ」があり，後者は跳躍不連続性を持つ：

における の微分可能性を求める：

差分商の極限が存在するので， は微分可能であり である：

のときの の極限は存在しないので，は不連続であることに注意のこと：

点における の微分可能性を求める：

x についての偏微分が存在する：

y についての偏微分も存在する：

しかし，線形化条件 lim_(r->r_0)(TemplateBox[{{{f, (, {x, ,, y}, )}, -, {f, (, {{x, _, 0}, ,, {y, _, 0}}, )}, -, {{p, (, {{x, _, 0}, ,, {y, _, 0}}, )}, ., {(, {r, -, {r, _, 0}}, )}}}}, RealAbs])/(TemplateBox[{{r, -, {r, _, 0}}}, Norm])=0は成り立たないので， は微分不可能である：

関数を可視化する：

の偏微分がいたるところに存在する点に注意のこと：

しかし，それらは点で不連続である：

導関数は差分商の極限として定義される：

第2導関数は2次差分商の極限を取ることで計算できる：

極限を取ることで混合偏微分 を直接計算する：

数学定数と式  (4)

Infinityにおける極限として を計算する：

原点における補極限：

Gamma関数の極限として を計算する：

Zeta関数を含む極限としてEulerGammaを計算する：

指数積分の極限としてEulerGammaを計算する：

その他の応用  (4)

関数 は における「little-o of 」と言われ，lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=0のとき と書かれる：

同様に， は「little-omega of と呼ばれ，lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=inftyのとき と書かれる：

であれば ：

2つの関数がどちらの関係も共有しないこともある：

さらに，どちらの関係もある関数とその関係の間で成り立たないこともある：

したがって， と は関数の半順序を定義する：

が よりも速くゼロに近付くなら ：

は逆の関係を表す：

とは比較できないので，2つのリストは完全な逆の関係ではない点に注意のこと：

テイラー(Taylor)の定理により， が の周りに 個の連続導関数を持つなら である：

次は，における5次テイラー多項式である：

の定義は lim_(x->a) TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]=0：

であることを確かめる：

特殊相対性では，質量 ，速度 の粒子の運動エネルギー以下で与えられる：

古典的な運動エネルギーの公式は以下である：

速度が0に近付くときの極限では，両方の式が一致する：

広義積分：

特性と関係  (14)

乗法定数は極限の外に動かすことができる：

f と g に有限極限があるなら，Limitは両者の和に配分される：

f と g に有限極限があるなら，Limitは両者の積に配分される：

ベキ乗は極限の外に出すことができる：

連続関数については，関数合成と数列極限操作を入れ替えることができる：

不連続関数については，上記が成り立たないかもしれない：

はさみうちの定理 （またはサンドイッチ定理）：

この関数は+/-TemplateBox[{x}, RealAbs]で有界である：

境界関数の極限はゼロである．これによってもともとの極限が0であったことが証明される：

原点における極限についての圧縮定理：

この関数は正の実軸上で について有界である：

境界関数の極限は0である．このことは，もともとの極限が0であったことを証明している：

Assumptionsは極限の式のパラメータに適用される：

Directionは極限変数に条件を設ける：

導関数は極限によって定義される：

比の極限はロピタル(L'Hôpital)の定理を使って計算されることが多い：

比を直接計算すると不定形0/0が与えられる：

比の極限はどう関数の比の極限に等しい：

この場合，f'と g'は連続的で，評価によって計算することができる：

Limitが存在するならDiscreteLimitも存在する．両者は同じ値である：

逆は成り立たなくてもよい：

Limitが存在するなら同じ値のMaxLimitも存在する：

Limitが存在するなら同じ値のMinLimitも存在する：

連続関数の極限は，定義域内の各点においてその関数の値と等しい：

FunctionContinuousを使って関数が連続的かどうかを調べる：

考えられる問題  (1)

Limitは，厳密ではない入力に対しては正しくない答を返すことがある：

厳密入力が使われた場合の結果は正しい：

不正な結果の原因は数値約分だった：

インタラクティブな例題  (1)

直径と垂直弦で囲まれた扇形の中で三角形が占める割合を求める：

円板の半怪が r のとき，水色の直角三角形の面積は以下の通りである：

同様に，着色した部分の総面積は扇形の面積から白い直角三角形の面積を引いたものである：

ϕ が0に近付くときの極限を計算する：

おもしろい例題  (2)

積分による微分：

極限集合を可視化する：

Wolfram Research (1988), Limit, Wolfram言語関数， https://reference.wolfram.com/language/ref/Limit.html （2017年に更新）.

テキスト

Wolfram Research (1988), Limit, Wolfram言語関数， https://reference.wolfram.com/language/ref/Limit.html （2017年に更新）.

CMS

Wolfram Language. 1988. "Limit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Limit.html.

APA

Wolfram Language. (1988). Limit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Limit.html

BibTeX

@misc{reference.wolfram_2024_limit, author="Wolfram Research", title="{Limit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/Limit.html}", note=[Accessed: 07-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_limit, organization={Wolfram Research}, title={Limit}, year={2017}, url={https://reference.wolfram.com/language/ref/Limit.html}, note=[Accessed: 07-November-2024 ]}