LinearFractionalOptimization
LinearFractionalOptimization[f,cons,vars]
線形制約 cons に従って線形分数目的関数 f を最小化する変数 vars の値を求める.
LinearFractionalOptimization[{α,β,γ,δ},{a,b}]
線形不等式制約 ![]() に従って線形分数関数
に従って線形分数関数![]() を最小化するベクトル
を最小化するベクトル ![]() を求める.
を求める.
LinearFractionalOptimization[{α,β,γ,δ},{a,b},{aeq,beq}]
線形等式制約 ![]() を含む.
を含む.
LinearFractionalOptimization[{α,β,γ,δ},…,{dom1,dom2,…}]
LinearFractionalOptimization[…,"prop"]
解のどの特性"prop"を返すべきか指定する.
詳細とオプション




- 線形分数最適化は線形分数計画法(LFP)および混合整数線形分数計画法(MILFP)としても知られている.
- 線形分数最適化は,実変数,整数変数あるいは複素変数で大域的に効率よく解くことができる凸最適化問題である.
- 線形分数最適化は主問題を解く
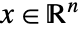 を求める. »
を求める. » -
最小化 
制約条件 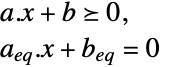
ただし 
- 混合整数線形部分最適化は,問題を解く
 および
および 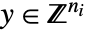 を求める.
を求める. -
最小化 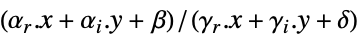
制約条件 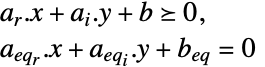
ただし 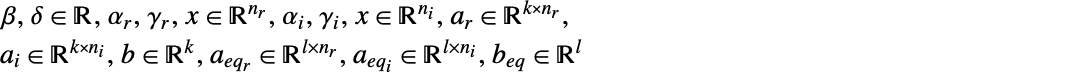
- LinearFractionalOptimizationは,目的関数が実数値のときは内部的に実変数
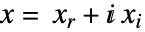 に変換して
に変換して ![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/LinearFractionalOptimization.ja/16.png) の問題を解く.ただし,
の問題を解く.ただし,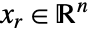 で
で 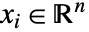 である,
である, - 変数指定 vars は,次のいずれかの形式で変数を与える要素のリストでなければならない.
-
v 名前が 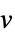 で次元が推測される変数
で次元が推測される変数v∈Reals 実数のスカラー変数 v∈Integers 整数のスカラー変数 v∈Complexes 複素数のスカラー変数 v∈ℛ 幾何学領域  に制限されたベクトル変数
に制限されたベクトル変数v∈Vectors[n,dom]  または
または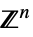 のベクトル変数
のベクトル変数v∈Matrices[{m,n},dom] 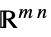 または
または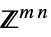 の行列変数
の行列変数 - 制約条件 cons は以下で指定できる.
-
LessEqual 
スカラー不等式 GreaterEqual 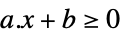
スカラー不等式 VectorLessEqual 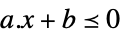
ベクトル不等式 VectorGreaterEqual 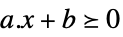
ベクトル不等式 Equal 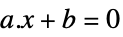
スカラー等式またはベクトル等式 Element 
凸領域または領域要素 - LinearFractionalOptimization[f,cons,vars]のとき,f または cons で使われるパラメータを定義するために,制約条件には parval の形式のパラメータ等式が含まれるかもしれない.ただし,par は vars には含まれず,val は数値または数値配列である.
- 主最小化問題には関連する最大化問題(ラグランジュ双対問題)がある.双対最大値は常に主最小値以下なので,下界を与える.双対マキシマイザは,制約条件に対する最小値の感度変化を含む,主問題についての情報を与える.
- 線形分数最適化のラグランジュ双対問題は以下で与えられる. »
-
最大化 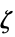
制約条件 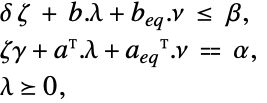
ただし 
- 線形分数最適化については,強双対性が常に成り立つ.つまり,主最小化問題に解があれば双対最大化問題にも解があり,双対最大値は主最小値に等しい.
- 可能な解の特性"prop"には以下がある.
-
"PrimalMinimizer" 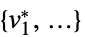
目的関数を最小化する変数値のリスト "PrimalMinimizerRules" 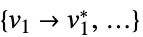
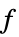 を最小化する変数の値 vars={v1,…}
を最小化する変数の値 vars={v1,…}"PrimalMinimizerVector" 
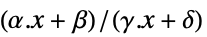 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 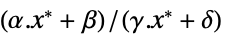
最小値 
"DualMaximizer" 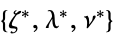
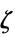 を最大化するベクトル
を最大化するベクトル"DualMaximumValue" 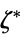
双対最大値 "DualityGap" 
双対最適値と主最適値の差(強双対性により0) "Slack" 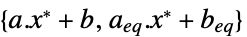
- 制約条件スラックベクトル
"ConstraintSensitivity" 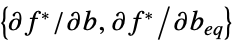
制約条件の摂動に対する 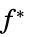 の感度
の感度"LinearFractionalObjectiveCoefficients" 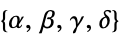
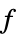 における係数
における係数"LinearInequalityConstraints" 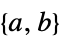
線形不等式制約の行列およびベクトル "LinearEqualityConstraints" 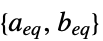
線形等式制約の行列およびベクトル {"prop1","prop2",…} いくつかの解の特性 - 双対最大値
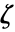 は
は 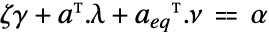 を介して
を介して  および
および  と関連がある.
と関連がある. - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの局面について最適化するか Tolerance Automatic 内部計算の許容度 WorkingPrecision Automatic 内部計算の精度 - オプションMethod->method を使って使用するメソッドを指定することができる.次は使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する "Simplex" シンプレックス法 "RevisedSimplex" 改訂シンプレックス法 "InteriorPoint" 内点法(機械精度のみ) "CLP" COINライブラリ線形計画法(機械精度のみ) "MOSEK" 商用MOSEK線形最適化ソルバ "Gurobi" 商用Gurobi線形最適化ソルバ "Xpress" 商用Xpress線形最適化ソルバ - WorkingPrecision->Automaticのときは,機械精度でしか使えないメソッドが指定されていない限り,入力引数の精度から自動的に精度が取られる.機械精度でしか使えないメソッドには機械精度が使用される.
- 求める解の分母が正か負のどちらであるか先験的に分かっているなら,分母の正または負と等しい定数 a または b を含むことでLinearFractionalOptimizationが解をより速く計算できるようになる.
例題
すべて開くすべて閉じる例 (3)
スコープ (33)
基本的な用法 (17)
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表現する:
VectorGreaterEqualを使っていくつかの GreaterEqual不等式制約を一度に表現する:
Equalを使っていくつかの不等式条件を一度に表現する:
スカラー不等式とベクトル不等式を組み合せて制約条件を指定する:
Indexedを使ってベクトル変数の成分,例えば ![]() にアクセスする:
にアクセスする:
定数パラメータ方程式を使って目的関数と制約条件の係数を指定する:
定数パラメータ方程式を使っていくつかの制約条件の係数を指定する:
必要なときは,Vectors[n]を使ってベクトル変数の次元を指定する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
スカラー,ベクトル,行列を指定することで,![]() に従って
に従って![]() を最小化する:
を最小化する:
整数変数 (4)
Integersを使って整数領域制約を指定する:
Vectors[n,Integers]を使ってベクトル変数についての整数領域制約を指定する:
NonNegativeIntegers (![]() )を使って非負の整数領域制約を指定する:
)を使って非負の整数領域制約を指定する:
NonPositiveIntegers (![]() )を使って非正の整数領域制約を指定する:
)を使って非正の整数領域制約を指定する:
主モデル特性 (3)
双対モデル特性 (3)
オプション (8)
Method (4)
MachinePrecisionのデフォルトメソッドは"CLP"である:
任意または無限のWorkingPrecisionのデフォルトメソッドは"Simplex"である:
MachinePrecision入力にはすべてのメソッドが使える:
"Simplex"と"RevisedSimplex"は任意精度および無限精度の入力に使える:
一般に,メソッドによって長所が異なる.これは,問題や実装によって異なる:
"Simplex"と"RevisedSimplex"は小さい密な問題に適している:
"InteriorPoint"と"CLP"は大きい疎な問題に適している:
最適解集合が一意ではない問題については,メソッドによって結果が異なることがある:
Tolerance (2)
WorkingPrecision (2)
アプリケーション (16)
基本的なモデリング変換 (6)
輸送問題 (1)
生産計画 (1)
資源配分 (1)
ある会社が,都市のピーク時の需要を満たしつつ利益を最大にして費用を最小にするために3つの発電所から4つの都市に送らなければならない電力量を求める.各発電所からさまざまな都市への百万kwの電力の1時間あたりの送電費用は以下の通りである:
各都市に毎時百万キロワットの電力を売ることで各発電所が生み出す利益は以下の通りである:
![]() は発電所
は発電所 ![]() から都市
から都市 ![]() に送られる電力量とする.電力の総輸送費用は
に送られる電力量とする.電力の総輸送費用は ![]() で,Inactive[Times]を使って構築できる:
で,Inactive[Times]を使って構築できる:
電力会社の総利益は ![]() で,Inactive[Times]を使って構築できる:
で,Inactive[Times]を使って構築できる:
都市のピーク時の需要量は,それぞれ毎時4500万kw, 2000万kw, 3000万kw, 3000万kwである:
発電所は最低でもそれぞれ毎時 3500万kw, 5000万kw, 4000万kwの電力が供給できる:
発電所は電力を供給するだけで,都市から電力を受け取ることはできない:
混合問題 (1)
投資問題 (2)
集合被覆問題 (3)
病院の救急救命室(ER)でリストにある処置を行うためにERに待機させなければならない医師の組合せを求める.各医師は特定数の処置しか行えないものとする:
各医師を待機させておくための(1時間あたりの)費用は以下の通りである:
![]() を医師
を医師 ![]() が待機している場合に
が待機している場合に ![]() となるような決定ベクトルとする.目的は費用を最小にしてERで待機する医師数を最大にすることである:
となるような決定ベクトルとする.目的は費用を最小にしてERで待機する医師数を最大にすることである:
6つの地区からなる都市に,各地区から15分以内の場所に消防署があるようにするために建設しなければならない消防署の最低数を求める.ある地区から隣の地区までの運転時間は以下の通りである:
各地区に消防署を建設する費用(100万ドル単位)は以下の通りである:
![]() を,地区
を,地区 ![]() に消防署が建設された場合に
に消防署が建設された場合に ![]() となるような決定ベクトルとする.目的は消防署の数を最大にして費用を最小にすることである:
となるような決定ベクトルとする.目的は消防署の数を最大にして費用を最小にすることである:
各地区から15分以内の場所に少なくとも1つの消防署がなければならない:
ある会社がその6つの小売店に商品を供給するために建設しなければならない倉庫の最小数を求める.この会社は倉庫の候補地を5つ選んだ.各小売店に各倉庫から商品を供給するための費用は以下の通りである:
![]() を,倉庫
を,倉庫 ![]() が建設されたなら
が建設されたなら ![]() となる決定変数とする.
となる決定変数とする.![]() は倉庫
は倉庫 ![]() が小売店
が小売店 ![]() に供給する商品の割合を表す.総費用は以下の通りである:
に供給する商品の割合を表す.総費用は以下の通りである:
特性と関係 (5)
LinearFractionalOptimizationは目的関数の大域的最小値を与える:
Minimizeは,線形分数最適化の大域的厳密結果も与える:
NMinimizeを使って大域メソッドを使って非厳密結果を得ることができる:
FindMinimumを使い,局所メソッドを使って非厳密結果を得ることができる:
考えられる問題 (6)
狭義不等式を使って指定された制約条件は満足されないことがある:
ミニマイザはIndeterminateである:
ミニマイザはIndeterminateである:
混合整数問題についての双対関連の解特性は得られないかもしれない:
複素数値を含む制約条件はベクトル不等式で指定しなければならない:
GreaterEqualあるいはLessEqualだけを使ってもうまくいかない:
テキスト
Wolfram Research (2019), LinearFractionalOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html (2020年に更新).
CMS
Wolfram Language. 2019. "LinearFractionalOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html.
APA
Wolfram Language. (2019). LinearFractionalOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html