LinearFractionalOptimization
LinearFractionalOptimization[f,cons,vars]
求能最小化受线性约束条件 cons 限制的线性分式目标函数 f 的变量 vars 的值.
LinearFractionalOptimization[{α,β,γ,δ},{a,b}]
求能最小化受线性不等式约束条件 ![]() 限制的线性分式函数
限制的线性分式函数 ![]() 的向量
的向量 ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},{a,b},{aeq,beq}]
包括线性等式约束条件 ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},…,{dom1,dom2,…}]
LinearFractionalOptimization[…,"prop"]
指定应返回解的 "prop" 属性.
更多信息和选项




- 线性分式优化也称为线性分式规划(LFP)和混合整数分式线性规划(MILFP).
- 线性分式优化是一个凸优化问题,可用实数、整数或复数变量高效地进行全局求解.
- 线性分式优化求可解决原始问题的
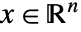 : »
: » -
最小化 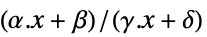
受限于约束条件 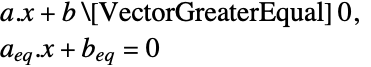
其中 
- 混合整数线性分式优化发现
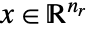 和
和 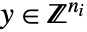 求解这个问题:
求解这个问题: -
最小化 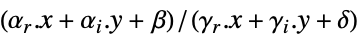
受限于约束条件 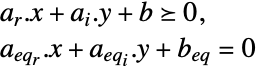
其中 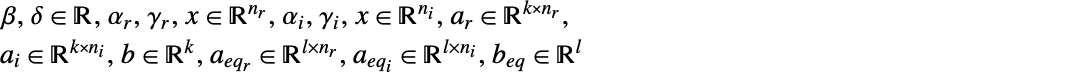
- 当目标函数取实数值时,LinearFractionalOptimization 在内部将
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/LinearFractionalOptimization.zh/15.png) 转换为实变量
转换为实变量 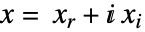 (其中
(其中 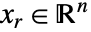 ,
,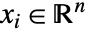 ),进行问题求解.
),进行问题求解. - 变量规范 vars 应该是一个列表,其中的元素以下列形式之一给出变量:
-
v 名称为 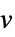 和推断维度的变量
和推断维度的变量v∈Reals 实数标量变量 v∈Integers 整数标量变量 v∈Complexes 复标量变量 v∈ℛ 仅限于几何区域 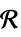 的向量变量
的向量变量v∈Vectors[n,dom] 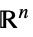 或
或  中的向量变量
中的向量变量v∈Matrices[{m,n},dom] 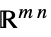 或
或 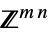 中的矩阵变量
中的矩阵变量 - 可用以下形式指定约束条件 cons:
-
LessEqual 
标量不等式 GreaterEqual 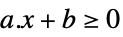
标量不等式 VectorLessEqual 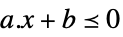
向量不等式 VectorGreaterEqual 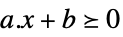
向量不等式 Equal 
向量或标量等式 Element 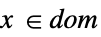
凸域或区域元素 - 对于 LinearFractionalOptimization[f,cons,vars],可在约束条件中包括形式为 parval 的参数方程,以定义在 f 或 cons 中使用的参数,其中 par 不在 vars 中,val 是数值或数值数组.
- 原始最小化问题有相关的最大化问题,即拉格朗日对偶问题. 对偶最大值始终小于或等于原始最小值,因此它给出了下限. 对偶最大值点提供了有关原问题的信息,包括最小值对约束条件变化的敏感性.
- 下面给出了线性分式优化的拉格朗日对偶问题: »
-
最大化 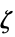
受限于约束条件 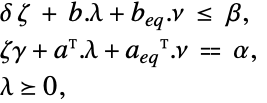
其中 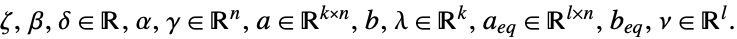
- 对于线性分式优化,强对偶性始终成立,这意味着如果原始最小化问题的解存在,那么对偶最大化问题的解也存在,并且对偶最大值等于原始最小值.
- 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 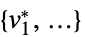
一个最小化目标函数的变量值列表 "PrimalMinimizerRules" 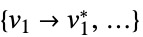
最小化  的变量值 vars={v1,…}
的变量值 vars={v1,…}"PrimalMinimizerVector" 
最小化 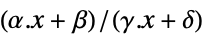 的向量
的向量"PrimalMinimumValue" 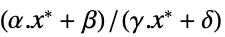
最小值 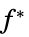
"DualMaximizer" 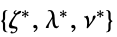
最大化 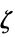 的向量
的向量"DualMaximumValue" 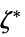
对偶最大值 "DualityGap" 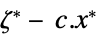
对偶值和原始最优值之间的差(由于强对偶性,差应为 0) "Slack" 
- 约束松弛向量
"ConstraintSensitivity" 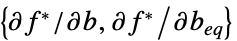
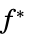 对约束条件扰动的敏感性
对约束条件扰动的敏感性"LinearFractionalObjectiveCoefficients" 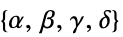
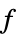 的系数
的系数"LinearInequalityConstraints" 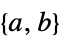
线性不等式约束矩阵和向量 "LinearEqualityConstraints" 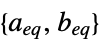
线性等式约束矩阵和向量 {"prop1","prop2",…} 解的几个属性 - 对偶最大值
 与
与  和
和  有关,关系式为
有关,关系式为 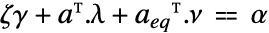 .
. - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较采用的容差 WorkingPrecision Automatic 内部计算使用的精度 - 选项 Method->method 可用来指定使用的方法. 可用的方法包括:
-
Automatic 自动选择方法 "Simplex" 单纯形法 "RevisedSimplex" 修正单纯形法 "InteriorPoint" 内点法(仅适用于机器精度) "CLP" COIN 库线性规划(仅适用于机器精度) "MOSEK" 商业 MOSEK 线性优化求解器 "Gurobi" 商业 Gurobi 线性优化求解器 "Xpress" 商业 Xpress 线性优化求解器 - 当设置为 WorkingPrecision->Automatic 时,精度是从输入参数的精度自动获取的,除非指定的方法仅适用于机器精度,在这种情况下使用机器精度.
- 如果先验已知所寻求的解的分母的正负,那么在 a 和 b 中放入规定分母正负的约束条件将加快 LinearFractionalOptimization 算出解的速度.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (33)
基本用法 (17)
用 VectorLessEqual 同时表示几个 LessEqual 不等式约束条件:
用 VectorGreaterEqual 同时表示几个 GreaterEqual 不等式约束条件:
用 Equal 同时表示几个等式约束条件:
用 Indexed 指定向量变量的分量,如 ![]() :
:
需要的情况下用 Vectors[n] 指定向量变量的维度:
用 NonNegativeReals (![]() ) 指定非负约束条件:
) 指定非负约束条件:
用 NonPositiveReals (![]() ) 指定非正约束条件:
) 指定非正约束条件:
整数变量 (4)
用 Integers 指定整数域约束条件:
用 Vectors[n,Integers] 指定向量变量的整数域约束条件:
用 NonNegativeIntegers (![]() ) 指定非负整数域约束条件:
) 指定非负整数域约束条件:
用 NonPositiveIntegers (![]() ) 指定非正整数域约束条件:
) 指定非正整数域约束条件:
原始模型属性 (3)
对偶模型属性 (3)
选项 (8)
Method (4)
MachinePrecision 情况下的默认方法是 "CLP":
任意或无限 WorkingPrecision 情况下的默认方法是 "Simplex":
所有方法都适用于 MachinePrecision 的输入:
"Simplex" 和 "RevisedSimplex" 可被用于任意精度和无限精度的输入:
"Simplex" 和 "RevisedSimplex" 适用于规模小且密集的问题:
"InteriorPoint" 和 "CLP" 适用于规模大且稀疏的问题:
如果问题的最优解集不是唯一的,不同的方法可能会给出不同的结果:
Tolerance (2)
WorkingPrecision (2)
应用 (16)
基本模型转换 (6)
运输问题 (1)
计划生产 (1)
资源分配 (1)
混合问题 (1)
投资问题 (2)
集合覆盖问题 (3)
求医院急诊室必须待命的医生的最佳组合,以便急诊室可以完成一系列手术. 每位医生只能完成一定数量的手术:
令 ![]() 为决策变量,如果医生
为决策变量,如果医生 ![]() 待命则
待命则 ![]() . 目标是最大程度地降低成本,同时使急诊室中医生的总数最大化:
. 目标是最大程度地降低成本,同时使急诊室中医生的总数最大化:
给出一个包含六个区的城市必须建立的最佳消防站数量,以使每个区 15 分钟之内至少有一个消防站. 在各区之间行驶所需的时间为:
令 ![]() 为决策变量,如果在城区
为决策变量,如果在城区 ![]() 建消防站则
建消防站则 ![]() . 目标是建最大数量的消防站,同时最小化成本:
. 目标是建最大数量的消防站,同时最小化成本:
求公司需要建立的最佳配送仓库的数量,以便为六个零售商店配送货物. 该公司选择了五个可能的地点. 每个仓库为每个商店配送货物的成本为:
令 ![]() 为决策变量,如果要建造仓库
为决策变量,如果要建造仓库 ![]() 则
则 ![]() . 令
. 令 ![]() 表示仓库
表示仓库 ![]() 提供给商店
提供给商店 ![]() 的商品份额. 总费用为:
的商品份额. 总费用为:
属性和关系 (5)
LinearFractionalOptimization 给出目标函数的全局最小值:
Minimize 也可给出线性分式优化问题的全局精确结果:
NMinimize 可用来通过全局方法获取非精确结果:
FindMinimum 可用来通过局部方法获取非精确结果:
可能存在的问题 (6)
文本
Wolfram Research (2019),LinearFractionalOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html (更新于 2020 年).
CMS
Wolfram 语言. 2019. "LinearFractionalOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html.
APA
Wolfram 语言. (2019). LinearFractionalOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html 年