WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

LogitModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

の形式の，各 xiに yiをフィットする二項ロジスティック回帰モデルを構築する．

LogitModelFit[data,{f1,…},{x1,x2,…}]

の形式の二項ロジスティック回帰モデルを構築する．ただし，fiは変数 xkに依存する．

LogitModelFit[{m,v}]

計画行列 m と応答ベクトル v から二項ロジスティック回帰モデルを構築する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
データ  
特性  
データとフィットされた関数  
残差  
分散と逸脱度  
パラメータ推定診断  
影響力の統計量  
予測値  
適合度尺度  
一般化と拡張  
オプション  
ConfidenceLevel  
CovarianceEstimatorFunction  
DispersionEstimatorFunction  
Show More Show More
IncludeConstantBasis  
LinearOffsetFunction  
NominalVariables  
Weights  
WorkingPrecision  
特性と関係  
考えられる問題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

LogitModelFit

LogitModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

の形式の，各 xiに yiをフィットする二項ロジスティック回帰モデルを構築する．

LogitModelFit[data,{f1,…},{x1,x2,…}]

の形式の二項ロジスティック回帰モデルを構築する．ただし，fiは変数 xkに依存する．

LogitModelFit[{m,v}]

計画行列 m と応答ベクトル v から二項ロジスティック回帰モデルを構築する．

詳細とオプション

  • LogitModelFitは，ロジスティックシグモイド関数によって構築された基底関数の線形結合を使ってデータをモデル化しようとする．
  • LogitModelFitは，通常，確率値をモデル化するために分類で使われる．
  • LogitModelFitは，もとの 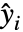は確率 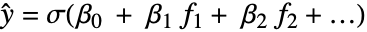のベルヌーイ(Bernoulli)試行の独立した実現であるという仮定のもとに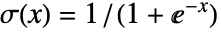，という形式の一般化された線形モデルを生成する．
  • 関数 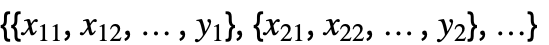はLogisticSigmoidである．
  • LogitModelFitは，自身が構築したロジスティックモデルを表す記号的なFittedModelオブジェクトを返す．モデルの特性と診断は model["property"]で得ることができる．
  • 特定の点 x1, …におけるLogitModelFitからの最もよくフィットした関数の値は model[x1,…]で得ることができる．
  • 次は，data の可能な形である．
  • {y1,y2,…}{{1,y1},{2,y2},…}という形式に等しい
    {{x11,x12,…,y1},…}独立した値 xijと応答 yiのリスト
    {{x11,x12,…}y1,…}入力値と応答の間の規則のリスト
    {{x11,x12,…},…}{y1,y2,…}入力値のリストと応答の間の規則
    {{x11,…,y1,…},…}n行列の第 n 列をフィットする
    Tabular[…]name表形式オブジェクトの列 name をフィットする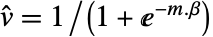
  • {{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}のような多変量のデータの場合，座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない．
  • yiは0から1までの確率である．
  • さらに，data は，関数および変数を指定しなくても計画行列を使って指定できる．
  • {m,v}計画行列 m と対応ベクトル v
  • LogitModelFit[{m,v}]では，{{f1,f2,…},{f1,f2,…},…}という形のデータ点における基底関数 fiの値から計画行列 m が形成される．応答ベクトル v は応答のリスト{y1,y2,…}である．
  • 計画行列 m と応答ベクトル v について，モデルは 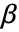である．ただし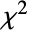， は推定されるパラメータのベクトルである．
  • 計画行列が使われる場合，基底関数 fiはLogitModelFit[{m,v},{f1,f2,…}]という形式を使って指定することができる．
  • LogitModelFitは，ExponentialFamily->"Binomial"およびLinkFunction->AutomaticでGeneralizedLinearModelFitに等しい．
  • LogitModelFitにはExponentialFamilyとLinkFunctionを除いてGeneralizedLinearModelFitと同じオプションが使える．

例題

すべて開く すべて閉じる

例  (1)

データ集合を定義する：

Wolfram Language code: data = {{1, 0}, {2, 0}, {2, 0}, {2, 1}, {2, 0}, {3, 0}, {3, 0}, {3, 0}, {3, 1}, {3, 1}, {3, 1}, {4, 1}, {4, 1}, {5, 0}, {6, 1}, {7, 1}};

ロジスティックモデルをデータにフィットする：

Wolfram Language code: logit = LogitModelFit[data, x, x]

ある点でモデルを評価する：

Wolfram Language code: logit[1.5]

データ点とモデルをプロットする：

Wolfram Language code: Show[ListPlot[data, PlotStyle -> PointSize[Medium]], Plot[logit[x], {x, 0, 8}]]

スコープ  (13)

データ  (6)

整数に依存しない値が増加すると仮定して，データを成功確率応答にフィットする：

Wolfram Language code: LogitModelFit[{1 / 3, 2 / 3, 5 / 5}, x, x]//Normal

これは以下に等しい：

Wolfram Language code: LogitModelFit[{{1, 1 / 3}, {2, 2 / 3}, {3, 5 / 5}}, x, x]//Normal

各予測器の値について，観測数によって重みを付ける：

Wolfram Language code: LogitModelFit[{{1, 1 / 3}, {2, 2 / 3}, {3, 5 / 5}}, x, x, Weights -> {3, 6, 5}]//Normal

以下は，成功失敗データと同じ最適フィット関数を与える：

Wolfram Language code: sfdata = {{1, 0}, {1, 1}, {1, 0}, {2, 0}, {2, 0}, {2, 1}, {2, 1}, {2, 1}, {2, 1}, {3, 1}, {3, 1}, {3, 1}, {3, 1}, {3, 1}}; GroupBy[sfdata, First -> Last]
Wolfram Language code: LogitModelFit[sfdata, x, x] //Normal

規則のリストをフィットする：

Wolfram Language code: LogitModelFit[{1 -> 1 / 3, 2 -> 2 / 3, 3 -> 3 / 3}, x, x]

入力値と応答の規則をフィットする：

Wolfram Language code: LogitModelFit[{1, 2, 3} -> {1 / 3, 2 / 3, 3 / 3}, x, x]

列を応答として指定する：

Wolfram Language code: data = {...};
Wolfram Language code: fit = LogitModelFit[data -> 1, {1, x, y}, {x, y}]
Wolfram Language code: Show[ Plot3D[fit[x, y], {x, -5, 5}, {y, -5, 5}], ListPointPlot3D[data[[All, {2, 3, 1}]]], PlotRange -> All ]

計画行列と応答ベクトルで与えられるモデルをフィットする：

Wolfram Language code: dm = {{1, 1}, {1, 2}, {1, 3}, {1, 4}}; resp = {0, 1, 0, 1};LogitModelFit[{dm, resp}]

関数形を見る：

Wolfram Language code: Normal[%]

基底関数を x とy として参照するモデルをフィットする：

Wolfram Language code: LogitModelFit[{dm, resp}, {x, y}]//Normal

使用可能な特性のリストを得る：

Wolfram Language code: logit = LogitModelFit[RandomReal[1, 10], x, x]
Wolfram Language code: logit["Properties"]

特性  (7)

データとフィットされた関数  (1)

ロジットモデルをフィットする：

Wolfram Language code: data = Join[RandomReal[10, {10, 2}], Transpose[{RandomReal[1, 10]}], 2];
Wolfram Language code: logit = LogitModelFit[data, {x, y}, {x, y}]

もとのデータを抽出する：

Wolfram Language code: logit["Data"]

最高のフィットを求め，プロットする：

Wolfram Language code: fit = logit["BestFit"]
Wolfram Language code: Show[Plot3D[fit, {x, 0, 10}, {y, 0, 10}], Graphics3D[{PointSize[0.025], Point[logit["Data"]]}]]

フィットされた関数を純関数として得る：

Wolfram Language code: logit["Function"]

フィッティングの計画行列と応答ベクトルを得る：

Wolfram Language code: MatrixForm /@ logit[{"DesignMatrix", "Response"}]

残差  (1)

フィットの残差を調べる：

Wolfram Language code: data = Join[RandomReal[10, {100, 2}], Transpose[{RandomReal[1, 100]}], 2];
Wolfram Language code: logit = LogitModelFit[data, {x, y}, {x, y}]
Wolfram Language code: {fr, ar, spr} = logit[{"FitResiduals", "StandardizedPearsonResiduals", "AnscombeResiduals"}];

生の残差を可視化する：

Wolfram Language code: ListPlot[fr]

ステムプロットでアンスコム(Anscombe)残差と標準化されたピアソン(Pearson)残差を可視化する：

Wolfram Language code: Map[ListPlot[#, Filling -> 0]&, {ar, spr}]

分散と逸脱度  (1)

ロジットモデルをデータにフィットする：

Wolfram Language code: SeedRandom[1]; data = Flatten[Table[{x, y, 1 / (1 + Exp[.2 + .3x + .1y + RandomReal[{-1, 1}]])}, {x, RandomReal[5, 10]}, {y, RandomReal[5, 10]}], 1];logit = LogitModelFit[data, {x, y}, {x, y}]

推定分散はデフォルトでは1である：

Wolfram Language code: logit["EstimatedDispersion"]

ピアソンの を推定分散として代りに使う：

Wolfram Language code: logit["EstimatedDispersion", DispersionEstimatorFunction -> "PearsonChiSquare"]

各点の逸脱度をプロットする：

Wolfram Language code: ListPlot[logit["Deviances"], Filling -> 0]

逸脱度分析表を得る：

Wolfram Language code: logit["DevianceData"]

表から逸脱度残差を得る：

Wolfram Language code: logit["DevianceData"][All, "ResidualDeviance"]//Normal

パラメータ推定診断  (1)

パラメータ情報のフォーマットされた表を得る：

Wolfram Language code: SeedRandom[1]; data = Table[{i, RandomInteger[BinomialDistribution[20, .05 + i / 30 + Sin[i] / 10]] / 20}, {i, 1, 20, .2}]; logit = LogitModelFit[data, {x, Sin[x], Cos[x]}, x];
Wolfram Language code: logit["ParameterEstimates"]

統計値の列を抽出する：

Wolfram Language code: logit["ParameterEstimates"][All, "ZStatistic"]//Normal

影響力の統計量  (1)

極値を含むデータをロジットモデルにフィットする：

Wolfram Language code: SeedRandom[3];data = Table[{i, 1 / (1 + Exp[2 + 4i - Log[i] + RandomReal[]])}, {i, RandomReal[{1, 10}, 20]}]; data[[{3, 8}, -1]] = 1 - data[[{3, 8}, -1]];
Wolfram Language code: ListPlot[data]
Wolfram Language code: logit = LogitModelFit[data, {x, Log[x]}, x]

クック距離をチェックして大きく影響する点を確認する：

Wolfram Language code: ListPlot[logit["CookDistances"], PlotRange -> {0, All}, Filling -> 0]

ハット行列の診断要素をチェックしてフィットの点の影響を見積もる：

Wolfram Language code: ListPlot[logit["HatDiagonal"], PlotRange -> {0, All}, Filling -> 0]

予測値  (1)

ロジットモデルをフィットする：

Wolfram Language code: SeedRandom[3];data = Flatten[Table[{x, y, 1 / (1 + Exp[.3x - .5y + RandomReal[{-1, 1}]])}, {x, RandomReal[5, 3]}, {y, RandomReal[5, 3]}], 1];logit = LogitModelFit[data, {x, y}, {x, y}]

予測値を観測値に対してプロットする：

Wolfram Language code: ListPlot[Transpose[logit[{"Response", "PredictedResponse"}]], FrameLabel -> {"observed", "predicted"}, Frame -> True, Axes -> False]

適合度尺度  (1)

ロジットモデルの適合度尺度表を得る：

Wolfram Language code: SeedRandom[3];data = Flatten[Table[{i, j, RandomReal[10], 1 / (1 + Exp[30i - 10j + RandomReal[5]])}, {i, RandomReal[10, 5]}, {j, RandomReal[10, 5]}], 1];
Wolfram Language code: logit = LogitModelFit[data, {x, y, z}, {x, y, z}]
Wolfram Language code: Grid[Transpose[{#, logit[#]}&[{"AIC", "BIC", "LikelihoodRatioIndex", "PearsonChiSquare"}]], Alignment -> Left]

予測器変数のすべての部分集合について適合度尺度を計算する：

Wolfram Language code: sub = Table[Join[{i}, LogitModelFit[data, i, {x, y, z}][{"AIC", "BIC", "LikelihoodRatioIndex", "PearsonChiSquare"}]], {i, Subsets[{x, y, z}]}]

AICによってモデルにランクを付ける：

Wolfram Language code: Grid[Join[{{"Model", "AIC", "BIC", "LikelihoodRatioIndex", "PearsonChiSquare"}}, SortBy[sub, -#[[2]]&]]]

一般化と拡張  (1)

モデルの関数形に対して他の数学操作を行う：

Wolfram Language code: logit = LogitModelFit[Table[{i, RandomReal[{i - 1, i}] / 10}, {i, 10}], x, x]

記号積分と数値積分を行う：

Wolfram Language code: Integrate[logit[x], x]
Wolfram Language code: NIntegrate[logit[x], {x, 1, 5}]

モデルの特定の値を与える予測値を求める：

Wolfram Language code: FindRoot[logit[x] == .5, {x, 5}]

オプション  (8)

ConfidenceLevel  (1)

デフォルト設定では95%の信頼区間が与えられる：

Wolfram Language code: data = {{0, 1}, {1, 0}, {3, 1}, {5, 0}};
Wolfram Language code: logit = LogitModelFit[data, x, x]
Wolfram Language code: logit["ParameterEstimates"][All, "ConfidenceInterval"]//Normal

99%の信頼区間を使う：

Wolfram Language code: logit = LogitModelFit[data, x, x, ConfidenceLevel -> .99]
Wolfram Language code: logit["ParameterEstimates"][All, "ConfidenceInterval"]//Normal

FittedModelでレベルを90%に設定する：

Wolfram Language code: logit["ParameterEstimates", ConfidenceLevel -> .9][All, "ConfidenceInterval"]//Normal

CovarianceEstimatorFunction  (1)

ロジットモデルをフィットする：

Wolfram Language code: data = {{0, 1}, {1, 0}, {3, 1}, {5, 0}};
Wolfram Language code: logit = LogitModelFit[data, x, x]

期待情報行列を使って共分散行列を計算する：

Wolfram Language code: logit["CovarianceMatrix"]

代りに，観察された情報行列を使う：

Wolfram Language code: logit["CovarianceMatrix", CovarianceEstimatorFunction -> "ObservedInformation"]

DispersionEstimatorFunction  (1)

ロジットモデルをフィットする：

Wolfram Language code: data = {{1, 0}, {1, 1}, {1, 1}, {2, 0}, {2, 0}, {2, 1}, {2, 1}, {2, 1}, {2, 1}};
Wolfram Language code: logit = LogitModelFit[data, x, x]

共分散行列を計算する：

Wolfram Language code: logit["CovarianceMatrix"]

ピアソンの を使って分散を推定し共分散行列を計算する：

Wolfram Language code: logit["CovarianceMatrix", DispersionEstimatorFunction -> "PearsonChiSquare"]

IncludeConstantBasis  (1)

ロジットモデルをフィットする：

Wolfram Language code: data = {{0, 1}, {1, 0}, {3, 1}, {5, 0}};
Wolfram Language code: LogitModelFit[data, x, x]//Normal

定数項なしでモデルをフィットする：

Wolfram Language code: LogitModelFit[data, x, x, IncludeConstantBasis -> False]//Normal

LinearOffsetFunction  (1)

データをロジットモデルにフィットする：

Wolfram Language code: data = {{0, 1}, {1, 0}, {3, 1}, {5, 0}};
Wolfram Language code: LogitModelFit[data, x, x]//Normal

既知のSqrt[x]項でデータをモデルにフィットする：

Wolfram Language code: LogitModelFit[data, x, x, LinearOffsetFunction -> (Sqrt[#]&)]//Normal

NominalVariables  (1)

Wolfram Language code: data = {{a, 0, 0}, {b, 2, 1}, {a, 2, 0}, {b, 0, 1}, {a, 2, 1}, {b, 0, 0}};

第1変数を名義変数として扱ってデータをフィットする：

Wolfram Language code: nom = LogitModelFit[data, {x, y}, {x, y}, NominalVariables -> x]
Wolfram Language code: Normal[nom]

両方の変数を名義変数として扱う：

Wolfram Language code: LogitModelFit[data, {x, y}, {x, y}, NominalVariables -> All]//Normal

Weights  (1)

等しい重みを使ってモデルをフィットする：

Wolfram Language code: data = {{0, 1}, {1, 0}, {3, 1}, {5, 0}};
Wolfram Language code: LogitModelFit[data, x, x]//Normal

データ点に明示的な重みを与える：

Wolfram Language code: LogitModelFit[data, x, x, Weights -> {1, (1/2), (1/3), (1/4)}]//Normal

WorkingPrecision  (1)

WorkingPrecisionを使ってより高精度のパラメータ推定を得る：

Wolfram Language code: data = Table[{x, (10 - x) / 10}, {x, 10}]
Wolfram Language code: logit = LogitModelFit[data, x, x, WorkingPrecision -> 30]

フィットされた関数を得る：

Wolfram Language code: logit["BestFit"]

フィットの後，特性計算で精度を落とす：

Wolfram Language code: logit["BestFit", WorkingPrecision -> MachinePrecision]

特性と関係  (4)

デフォルト設定でのGeneralizedLinearModelFitからの"Binomial"モデルは LogitModelFitのモデルに等しい：

Wolfram Language code: data = Table[{i, RandomReal[{i - 1, i}] / 10}, {i, 10}];
Wolfram Language code: GeneralizedLinearModelFit[data, x, x, ExponentialFamily -> "Binomial"]//Normal
Wolfram Language code: LogitModelFit[data, x, x]//Normal

ProbitModelFitは"ProbitLink"を伴った"Binomial"モデルに等しい：

Wolfram Language code: GeneralizedLinearModelFit[data, x, x, ExponentialFamily -> "Binomial", LinkFunction -> "ProbitLink"]//Normal
Wolfram Language code: ProbitModelFit[data, x, x]//Normal

LogitModelFitは二項分布された応答を仮定する：

Wolfram Language code: data = Table[{i, RandomReal[{i - 1, i}] / 10}, {i, 10}];
Wolfram Language code: lm = LogitModelFit[data, x, x]

NonlinearModelFitは正規分布された応答を仮定する：

Wolfram Language code: nm = NonlinearModelFit[data, 1 / (1 + Exp[a + b x]), {a, b}, x]

このフィットは同一ではない：

Wolfram Language code: {Normal[lm], Normal[nm]}
Wolfram Language code: Plot[{lm[x], nm[x]}, {x, 1, 5}]

LogitModelFitはTimeSeriesのタイムスタンプを変数として使う：

Wolfram Language code: ts1 = TemporalData[TimeSeries, {{{0.7758532198866042, 0.20426632015371096, 0.2353690565215641, 0.4448009174525732, 0.5081575045542254, 0.5371908040104083, 0.6223323745794831, 0.669522447912184, 0.7204685251554224, 0.7633871517003976}}, {{0, 9, 1}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.1];
Wolfram Language code: ts1["Times"]
Wolfram Language code: LogitModelFit[ts1, x, x]

タイムスタンプを再スケールし，フィットし直す：

Wolfram Language code: ts2 = TimeSeriesRescale[ts1, {.1, 2}]
Wolfram Language code: ts2["Times"]
Wolfram Language code: LogitModelFit[ts2, x, x]

値についてのフィットを求める：

Wolfram Language code: LogitModelFit[ts1["Values"], x, x]

LogitModelFitは，複数の経路のあるTemporalDataについては，経路ごとに作用する：

Wolfram Language code: LogitModelFit[TemporalData[Automatic, {{{0.009753347177267509, 0.18455899093641098, 0.20260886672737863, 0.37977270854029854, 0.45927203330240407, 0.5010683896315415, 0.6468842072138713, 0.7452632634563319, 0.8683334166368966, 0.9876532168951402}, ... 2138713, 0.7452632634563319, 0.8683334166368966, 0.9876532168951402}}, {{0, 9, 1}, {0.1, 2., 0.2111111111111111}}, 2, {"Continuous", 2}, {"Discrete", 2}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.1], x, x]

考えられる問題  (1)

0から1までの範囲外の応答はロジットモデルには有効ではない：

Wolfram Language code: LogitModelFit[Range[5], x, x]
Wolfram Language code: LogitModelFit[Table[{i, 2i}, {i, 10}], x, x]
Wolfram Research (2008), LogitModelFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/LogitModelFit.html （2025年に更新）.

テキスト

Wolfram Research (2008), LogitModelFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/LogitModelFit.html （2025年に更新）.

CMS

Wolfram Language. 2008. "LogitModelFit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/LogitModelFit.html.

APA

Wolfram Language. (2008). LogitModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogitModelFit.html

BibTeX

@misc{reference.wolfram_2026_logitmodelfit, author="Wolfram Research", title="{LogitModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/LogitModelFit.html}", note=[Accessed: 16-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_logitmodelfit, organization={Wolfram Research}, title={LogitModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/LogitModelFit.html}, note=[Accessed: 16-July-2026]}