LucasL
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- The
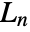 satisfy the recurrence relation
satisfy the recurrence relation 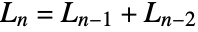 with
with 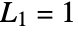 ,
, 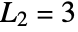 .
. - For any complex value of n the
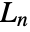 are given by the general formula
are given by the general formula 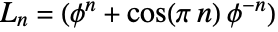 , where
, where 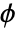 is the golden ratio.
is the golden ratio. - The Lucas polynomial
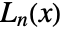 is the coefficient of
is the coefficient of 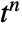 in the expansion of
in the expansion of 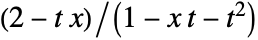 .
. - The Lucas polynomials satisfy the recurrence relation
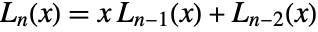 .
. - LucasL can be evaluated to arbitrary numerical precision.
- LucasL automatically threads over lists.
- LucasL can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (4)
Scope (39)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix LucasL function using MatrixFunction:
Specific Values (6)
Visualization (4)
Function Properties (14)
LucasL is defined for all real and complex values:
The range of ![]() is all real numbers for odd
is all real numbers for odd ![]() :
:
Its range over the complex plane is all complex numbers for any natural number ![]() :
:
Lucas polynomial of an odd order is odd:
Lucas polynomial of an even order is even:
LucasL has the mirror property ![]() :
:
LucasL threads elementwise over lists:
LucasL is neither non-decreasing nor non-increasing for even values:
LucasL is non-decreasing for odd values:
LucasL is not injective for even values:
LucasL is not surjective for even values:
LucasL is non-negative for even values:
LucasL does not have singularity nor discontinuity:
LucasL is convex for even values:
TraditionalForm formatting:
Differentiation (3)
Series Expansions (4)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Find the series expansion at Infinity:
Function Identities and Simplifications (2)
Lucas numbers are related to the Fibonacci numbers by the identities:
The ordinary generating function of LucasL:
Applications (6)
Solve the Fibonacci recurrence equation:
Find ratios of successive Lucas numbers:
Compare with continued fractions:
Convergence to the Golden Ratio:
Calculate the number of ways to write an integer as a sum of Lucas numbers ![]() :
:
Plot the counts for the first hundred integers:
Properties & Relations (10)
Expand in terms of elementary functions:
Explicit recursive definition:
Simplify some expressions involving Lucas numbers:
Extract Lucas numbers as coefficients:
LucasL can be represented as a DifferenceRoot:
General term in the series expansion of LucasL:
The generating function for LucasL:
FindSequenceFunction can recognize the LucasL sequence:
The exponential generating function for LucasL:
Possible Issues (2)
Text
Wolfram Research (2007), LucasL, Wolfram Language function, https://reference.wolfram.com/language/ref/LucasL.html (updated 2008).
CMS
Wolfram Language. 2007. "LucasL." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/LucasL.html.
APA
Wolfram Language. (2007). LucasL. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LucasL.html