MandelbrotSetPlot

MandelbrotSetPlot[{zmin,zmax}]

マンデルブロ集合の，コーナーが zminおよび zmaxである長方形に入る部分をプロットする．

MandelbrotSetPlot[]

マンデルブロ集合をデフォルトの長方形内にプロットする．

詳細とオプション

  • マンデルブロ集合は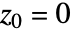，から始めた場合に，数列 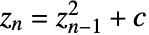が無限大に発散しないすべての複素数 c の集合である．
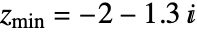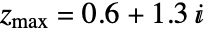  • MandelbrotSetPlot[]のデフォルトの長方形のコーナーは， および である．
  • MandelbrotSetPlotは，Rasterプリミティブを含むGraphicsオブジェクトを作る．
  • MandelbrotSetPlot[]には，Graphicsと同じオプションに次を加えたものが使える．
  • ColorFunction Automatic画素の色をどのように決定するか
    EscapeRadius 2点が集合に含まれないと，どのように決定するか
    FrameTrueプロットの周りに枠を描くかどうか
    ImageResolution 500大きい方の方向の画像の解像度
    MaxIterations 1000点ごとの最大反復回数
    PerformanceGoal$PerformanceGoalパフォーマンスのどの面について最適化するか
    PlotLegendsNone反復回数についての凡例
    PlotTheme $PlotThemeプロットの全体的なテーマ
  • MaxIterations->n（n は正の整数）のとき，関数 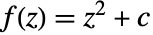は，0の軌道が2を超えるかどうかを判断するために，最高で n 回反復される．
  • ColorFunction->f（f は関数）のとき，f の引数は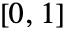の形の反復回数に比例する実数であり，f はRGBColorあるいはHueのような色指示子，またはRedあるいはBlueのような名前付きの色を返さなければならない．
  • ColorFunction->"name"はColorFunction->(If[#1,Black,ColorData["name"][#]]&)と等価である．
  • 使用可能な色関数名のリストはColorData["Gradients"]で得ることができる．

例題

すべて開くすべて閉じる

例  (3)

マンデルブロ集合全体を示す：

拡大し，色を変える：

反復回数の凡例を示す：

オプション  (9)

ColorFunction  (5)

スケールされた反復回数で色付けするために，組込みの色関数を使う：

組込みの色関数に変更を加える：

名前付きの色階調度を使う：

詳細と色を見るために拡大する：

カスタムの色関数を書く：

反復回数が10回未満のすべての点に彩色する：

EscapeRadius  (1)

エスケープ半径を大きくすると，色から色への変化が滑らかになる：

ImageResolution  (1)

より細かいプロットにするためにImageResolutionを上げる：

MaxIterations  (1)

MaxIterationsを大きくして拡大したときの質を向上させる：

PlotTheme  (1)

単純な目盛と明るいカラースキームのテーマを使う：

カラースキームを変える：

特性と関係  (3)

マンデルブロ集合中の点は二次ジュリア集合を決定する：

MandelbrotSetMemberQを使って，ある点がマンデルブロ集合に含まれるかどうかを調べる：

MandelbrotSetIterationCountは，点がマンデルブロ集合に含まれないかどうかを調べるために行った反復の回数を与える：

おもしろい例題  (1)

マンデルブロ集合の補色をチェス盤にする：

Wolfram Research (2014), MandelbrotSetPlot, Wolfram言語関数， https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.

テキスト

Wolfram Research (2014), MandelbrotSetPlot, Wolfram言語関数， https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.

CMS

Wolfram Language. 2014. "MandelbrotSetPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.

APA

Wolfram Language. (2014). MandelbrotSetPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html

BibTeX

@misc{reference.wolfram_2024_mandelbrotsetplot, author="Wolfram Research", title="{MandelbrotSetPlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mandelbrotsetplot, organization={Wolfram Research}, title={MandelbrotSetPlot}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html}, note=[Accessed: 17-November-2024 ]}