MandelbrotSetPlot
MandelbrotSetPlot[{zmin,zmax}]
在边角为 zmin 和 zmax 的长方形内绘制部分曼德尔布罗特集.
在默认长方形内绘制部分曼德尔布罗特集.
更多信息和选项

- 序列
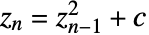 ,从
,从 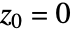 开始迭代,曼德尔布罗特集就是使序列不发散至无限大的所有复数 c 的集合.
开始迭代,曼德尔布罗特集就是使序列不发散至无限大的所有复数 c 的集合. - 默认的 MandelbrotSetPlot[] 长方形的边角为
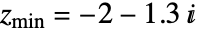 和
和 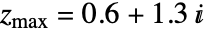 .
. - MandelbrotSetPlot 生成一个含有 Raster 基元的 Graphics 对象.
- MandelbrotSetPlot[] 和 Graphics 有同样的选项, 下面所示为增加的选项:
-
ColorFunction Automatic 怎样确定像素的颜色 EscapeRadius 2 怎样确定一个点是否属于曼德尔布罗特集合 Frame True 是否为图形加上边框 ImageResolution 500 在较大方向上图像的分辨率 MaxIterations 1000 每一个点上可进行迭代计算的次数 PerformanceGoal $PerformanceGoal 要优化的目标 PlotLegends None 迭代次数图例 PlotTheme $PlotTheme 图形的整体外观主题 - MaxIterations->n,其中 n 是一个正整数,将函数
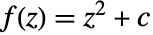 最多迭代计算 n 次,以确定0的轨道是否超过2.
最多迭代计算 n 次,以确定0的轨道是否超过2. - ColorFunction->f,其中 f 是一个函数,f 的参变量是一个范围为
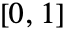 的实数,和迭代次数成比例,f 必须返回和颜色有关的指令,比如 RGBColor 和 Hue,或是颜色名称,比如 Red 和 Blue.
的实数,和迭代次数成比例,f 必须返回和颜色有关的指令,比如 RGBColor 和 Hue,或是颜色名称,比如 Red 和 Blue. - ColorFunction->"name" 等价于 ColorFunction->(If[#1,Black,ColorData["name"][#]]&).
- 可能的颜色函数名称列表由 ColorData["Gradients"] 给出.
范例
打开所有单元关闭所有单元选项 (9)
ColorFunction (5)
ImageResolution (1)
提高 ImageResolution 使图像更清晰:
MaxIterations (1)
增大 MaxIterations 提高放大显示时图像的质量:
属性和关系 (3)
用 MandelbrotSetMemberQ 来判断一个点是否属于曼德尔布罗特集合:
MandelbrotSetIterationCount 给出判断一个点是否属于曼德尔布罗特集合所需的迭代次数:
Wolfram Research (2014),MandelbrotSetPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.
文本
Wolfram Research (2014),MandelbrotSetPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.
CMS
Wolfram 语言. 2014. "MandelbrotSetPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.
APA
Wolfram 语言. (2014). MandelbrotSetPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html 年