Maximize

Maximize[f,x]

x について f を記号的に最大にする．

Maximize[f,{x,y,…}]

x, y, … について f を記号的に最大にする．

Maximize[{f,cons},{x,y,…}]

制約条件 cons 下で f を記号的に最大にする．

Maximize[…,x∈rdom]

x が領域 rdom 内にあるように制限する．

Maximize[…,…,dom]

変数を領域 dom（一般にRealsかIntegers）に制限する．

詳細とオプション

  • Maximizeは上限（シュープレマム），記号最適化，および大域的最適化(GO)としても知られている．
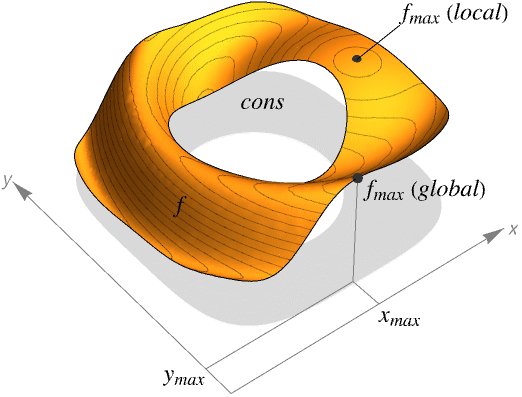
  • Maximizeは与えられた制約条件に従って f の最大値を求める．
  • Maximizeは，通常，制約条件下で可能な最大値を求めるために使われる．分野によっては，最適な戦略，最良適合，最適な構成等と呼ばれることがある．
  • Maximizeは{fmax,{x->xmax,y->ymax,…}}の形式のリストを返す．
  • f および cons が線形あるいは多項式の場合，Maximizeは常に大域的な最大値を求める．
  • 制約条件 cons は以下の論理結合でよい．
  • lhs==rhs等式
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs不等式 (LessEqual,…)
    lhsrhs, lhsrhs, lhsrhs, lhsrhsベクトル不等式 (VectorLessEqual,…)
    Exists[…], ForAll[…]量化条件
    {x,y,…}∈rdom領域指定
  • Maximize[{f,cons},x∈rdom]は，事実上，Maximize[{f,cons∧x∈rdom},x]に等しい．
  • x∈rdom については，Indexed[x,i]を使って別の座標に言及することができる．
  • 次は，使用可能な領域 rdom である．
  • Reals実数スカラー変数
    Integers整数スカラー変数
    Vectors[n,dom]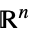のベクトル変数
    Matrices[{m,n},dom]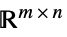の行列変数
    ℛ幾何領域 に制限されたベクトル変数
  • デフォルトで，すべての変数が実数であるとみなされる．
  • Maximizeは入力が厳密値の場合は厳密値を返す．入力が近似値の場合は自動的にNMaximizeを呼び出す．
  • Maximizeは次の形式を返す．
  • {fmax,{xxmax,…}}有限最大値
    {-∞,{xIndeterminate,…}}実行不可能，つまり，制約条件集合が空
    {∞,{xxmax,…}}非有界，つまり，f の値は任意に大きくできる
  • 最大値が制約条件で定義された領域外で無限小にあるいは漸近的にしか達しなかった場合，Maximizeは上限と最も近い指定可能な点を返す．
  • いくつかの点で同じ最大値に達したとしても，その中の1つしか返されない．
  • N[Maximize[…]]は，記号的には解けない最適化問題についてはNMaximizeを呼び出す．
  • Maximize[f,x,WorkingPrecision->n]は n 桁精度で結果を計算する． »

例題

すべて開くすべて閉じる

例  (5)

一変量関数を最大化する：

多変量関数を最大化する：

制約条件に従って関数を最大化する：

パラメータを含む最大化問題：

幾何学領域上で関数を最大化する：

これをプロットする：

スコープ  (36)

基本的な用法  (7)

制約条件のない実数上でを最大にする：

制約条件 に従って を最大にする：

制約条件は任意の論理結合を含むことがある：

非有界の問題：

実行不可能な問題：

上限値には達しないかもしれない：

ベクトル変数とベクトル不等式を使う：

一変数の問題  (7)

制約条件なしの一変量多項式の最大化：

制約条件付き一変量多項式の最大化：

指数対数関数：

有界の条件上での解析関数：

周期関数：

三角関数と通約可能な周期の組合せ：

周期関数と通約可能な周期の組合せ：

区分関数：

関数の特性情報を使って可解の制約条件がない問題：

多変数の問題  (9)

多変量線形制約条件付き最大化：

線形分数制約条件付き最大化：

制約条件なしの多項式の最大化：

制約条件付きの多項式の最適化は常に解くことができる：

最大値には達しないかもしれない：

目的関数は境界がないことがある：

制約条件を満足する点は存在しないかもしれない：

定量化された多項式制約：

代数的最大化：

境界付き超越方程式の最大化：

区分関数最大化：

凸最大化：

が半正定でとなるように凹目的関数を最大にする：

領域と最小化点をプロットする：

パラメトリック問題  (4)

パラメトリック線形最適化：

最大値はパラメータの連続関数である：

パラメトリック二次最適化：

最大値はパラメータの連続関数である：

制約条件なしのパラメトリック多項式最大化：

制約条件付きパラメトリック多項式最大化：

整数上の最適化  (3)

一変数問題：

整数線形計画法：

整数上での多項式最大化：

領域上の最適化  (6)

領域上で最大化する：

これをプロットする：

2領域における点の間の最大距離を求める：

これをプロットする：

三角形と楕円が交差するような，最大の を求める：

これをプロットする：

が指定された3点を含むような，最大の を求める：

これをプロットする：

を使って が 内のベクトルであると指定する：

2領域における点の間の最大距離を求める：

これをプロットする：

オプション  (1)

WorkingPrecision  (1)

厳密解を求めるのには時間がかかる：

WorkingPrecision->200とすると，厳密な最大値が得られるが，求まった最大値は正しくないかもしれない：

アプリケーション  (13)

基本的なアプリケーション  (3)

単位周を持つ長方形の最大面積を求める：

単位周を持つ三角形の最大面積を求める：

投射物によって達せられる最大の高さを求める：

投射物の最大範囲を求める：

幾何学的距離  (9)

領域 ℛ 内の点から指定された点 p までの最大距離と，最大距離を実現する点 q はMaximize[EuclideanDistance[p,q],q∈ℛ]で与えられる．単位Disk[]内の{1,1}からの最大距離と最も遠い点を求める：

これをプロットする：

標準的な単位シンプレックスSimplex[2]内の{1,3/4}からの最大距離と最も遠い点を求める：

これをプロットする：

標準的な単位球Sphere[]内の点{1,1,1}からの，最大距離と最も遠くにある点を求める：

これをプロットする：

標準的な単位シンプレックスSimplex[3]内の{-1/3,1/3,1/3}からの最大距離と最も遠くにある点を求める：

これをプロットする：

領域 ℛ の直径は，ℛ 内の2点間の最大距離である．ℛ の直径と，この領域内で最も遠くにある点のペアは Maximize[EuclideanDistance[p,q],{p∈ℛ,q∈ℛ}]で計算することができる．Circle[]の直径と，この中で最も遠くにある点のペアを求める：

これをプロットする：

標準的な単位シンプレックスSimplex[2]の直径と，この中で最も遠くにある点のペアを求める：

これをプロットする：

標準単位立方体Cuboid[]の直径と，この中で最も遠くにある点のペアを求める：

これをプロットする：

最も遠くにある点 p∈ と q∈，および両者の距離は，Maximize[EuclideanDistance[p,q],{p∈,q∈}]で求めることができる．Disk[{0,0}]とRectangle[{3,3}]で最も遠くにある点と両者の距離を求める：

これをプロットする：

Line[{{0,0,0},{1,1,1}}]とBall[{5,5,0},1]で最も遠くにある点と両者の距離を求める：

これをプロットする：

幾何学的中心  (1)

ℛ⊆nが全次元の領域の場合，Chebyshev center は ℛ の最大内接球の中心である．ℛ の最大内接球の中心と半径はMaximize[-SignedRegionDistance[ℛ,p], p∈ℛ]で求めることができる．Rectangle[]についての最大内接球のChebyshev Centerと半径を求める：

Triangle[]についてのChebyshev Centerと最大内接球の半径を求める：

特性と関係  (4)

Maximizeは，目的関数の厳密な大域的最大値を返す：

NMaximizeは，大域的最大値を数値的に求めようとするが，求まった最大値は極大値であることがある：

FindMaximumは初期値に依存して極大値を求める：

メッセージで特に指示がない限り，最大点は制約条件を満たす：

指定された点は点{2,}からの距離を最大化する：

最大値に達せない場合，Maximizeは境界上の点を返すことがある：

以下では y が無限大に近付くに従って目的関数が最大値に近付いている：

Maximizeは線形計画法問題を解くことができる：

LinearProgrammingを使って，行列で表された同じ問題を解くことができる：

次は最大値を計算する：

RegionBoundsを使って境界ボックスを計算する：

MaximizeおよびMinimizeを使って同じ境界を計算する：

考えられる問題  (1)

Maximizeの入力に使われる関数はすべて実数値を持たなければならない：

方程式は満足するが平方根が実数ではない値は許容されない：

Wolfram Research (2003), Maximize, Wolfram言語関数， https://reference.wolfram.com/language/ref/Maximize.html （2021年に更新）.

テキスト

Wolfram Research (2003), Maximize, Wolfram言語関数， https://reference.wolfram.com/language/ref/Maximize.html （2021年に更新）.

CMS

Wolfram Language. 2003. "Maximize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Maximize.html.

APA

Wolfram Language. (2003). Maximize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Maximize.html

BibTeX

@misc{reference.wolfram_2024_maximize, author="Wolfram Research", title="{Maximize}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Maximize.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maximize, organization={Wolfram Research}, title={Maximize}, year={2021}, url={https://reference.wolfram.com/language/ref/Maximize.html}, note=[Accessed: 21-November-2024 ]}