NExpectation[expr,xdist]
假定 x 服从概率分布 dist,给出 expr 的数值期望.
NExpectation[expr,{x1,x2,…}dist]
假定 {x1,x2,…} 服从多元分布 dist,给出 expr 的数值期望.
NExpectation[expr,{x1dist1,x2dist2,…}]
假定 x1、x2、… 独立且服从分布 dist1、dist2、…,给出 expr 的数值期望.
NExpectation[exprpred,…]
已知 pred,给出 expr 的数值条件期望.


NExpectation
NExpectation[expr,xdist]
假定 x 服从概率分布 dist,给出 expr 的数值期望.
NExpectation[expr,{x1,x2,…}dist]
假定 {x1,x2,…} 服从多元分布 dist,给出 expr 的数值期望.
NExpectation[expr,{x1dist1,x2dist2,…}]
假定 x1、x2、… 独立且服从分布 dist1、dist2、…,给出 expr 的数值期望.
NExpectation[exprpred,…]
已知 pred,给出 expr 的数值条件期望.
更多信息和选项

- xdist 可以用 x
 dist
dist dist 或 x \[Distributed]dist 输入.
dist 或 x \[Distributed]dist 输入. - exprpred 可以用 expr
 cond
cond pred 或 expr \[Conditioned]pred 输入.
pred 或 expr \[Conditioned]pred 输入. - NExpectation 与 Expectation 作用相似,只是使用的是数值加和与积分法.
- 对于一个连续分布 dist,expr 的期望由
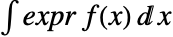 给出,其中
给出,其中 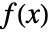 是 dist 的概率密度函数,并且积分在 dist 的定义域上进行.
是 dist 的概率密度函数,并且积分在 dist 的定义域上进行. - 对于一个离散分布 dist,expr 的期望由
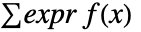 给出,其中
给出,其中 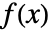 是 dist 的概率密度函数,并且加和在 dist 的定义域上进行.
是 dist 的概率密度函数,并且加和在 dist 的定义域上进行. - NExpectation[expr,{x1dist1,x2dist2}] 对应于 NExpectation[NExpectation[expr,x2dist2],x1dist1], 因此最后一个变量首先进行加和或积分.
- 如果无法得到符号式期望,N[Expectation[…]] 将调用 NExpectation.
- 可以给定下列选项:
-
AccuracyGoal ∞ 所求绝对准确度的位数 PrecisionGoal Automatic 所求精度的位数 WorkingPrecision MachinePrecision 内部计算所用的精度 Method Automatic 要使用何种方法 TargetUnits Automatic 输出中显示的的单位
范例
打开所有单元 关闭所有单元范围 (28)
基本用途 (9)
如果符合式计算失效,应用 N[Expectation[…]] 来调用 NExpectation:
数量用途 (4)
非参数分布 (2)
导出分布 (9)
利用 TransformedDistribution 计算期望:
利用 ProductDistribution 求期望:
选项 (7)
AccuracyGoal (1)
用 AccuracyGoal 得到不同准确度的结果:
Method (3)
PrecisionGoal (1)
使用 PrecisionGoal 来得到一个不同精度的结果:
WorkingPrecision (1)
默认情况下,NExpectation 使用机器精度:
利用 WorkingPrecision 得到具有较高精度的结果:
TargetUnits (1)
应用 (17)
精算科学 (4)
某保险单对损失的赔偿金额上限为 10. 保单持有人的损失 ![]() 服从密度函数为
服从密度函数为 ![]() (当
(当 ![]() )、在其它情况下为 0 的分布. 求在这个保险单下所支付的赔偿金额的预期值:
)、在其它情况下为 0 的分布. 求在这个保险单下所支付的赔偿金额的预期值:
使用一个连续的正随机变量 ![]() 对一个保险公司的月索赔情况建模,这个随机变量的概率密度函数与
对一个保险公司的月索赔情况建模,这个随机变量的概率密度函数与 ![]() 成正比,其中
成正比,其中 ![]() . 判断公司的期望月索赔:
. 判断公司的期望月索赔:
由风灾引起的受保险房屋的索赔金额是具有公共密度函数 ![]() (当
(当 ![]() )、在其它情况下为 0 的独立随机变量,其中
)、在其它情况下为 0 的独立随机变量,其中 ![]() 是以千为单位的索赔金额. 假定有3个此类索赔. 计算这三个索赔中最大值的期望值:
是以千为单位的索赔金额. 假定有3个此类索赔. 计算这三个索赔中最大值的期望值:
令 ![]() 表示在一次事故中受保险的机动车辆的年龄. 令
表示在一次事故中受保险的机动车辆的年龄. 令 ![]() 表示在事故发生时车主为车辆加入保险的时间长度.
表示在事故发生时车主为车辆加入保险的时间长度. ![]() 和
和 ![]() 的联合密度函数为
的联合密度函数为 ![]() (当
(当 ![]() 以及
以及 ![]() )、在其它情况下为 0. 计算事故中涉及的受保险的机动车辆的期望年龄:
)、在其它情况下为 0. 计算事故中涉及的受保险的机动车辆的期望年龄:
运动 (2)
随机试验 (2)
求三个最大值之和的期望. 使用恒等式 ![]() 以及所得 Expectation 的线性性:
以及所得 Expectation 的线性性:
一个服从连续分布 ![]() 的大小为 10 的样本按升序排列. 生成一个新的随机变量. 求第 11 个样本位于有序列表的第四和第五个最小数值之间的概率:
的大小为 10 的样本按升序排列. 生成一个新的随机变量. 求第 11 个样本位于有序列表的第四和第五个最小数值之间的概率:
风险分析 (2)
属性和关系 (7)
Mean、Moment、Variance 及其它性质定义为一个期望:
使用 Expectation 求一个期望的符号表达式:
如果符号式计算失败,N[Expectation[…]] 等价于 NExpectation:
用 AsymptoticExpectation 求期望的渐近近似:
利用 NExpectation 得到相同的结果:
可能存在的问题 (1)
当符号式参数出现时,NExpectation 可能会在不发出警告信息的情况下失效:
此例中,Expectation 给出解析形式的结果:
文本
Wolfram Research (2010),NExpectation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NExpectation.html.
CMS
Wolfram 语言. 2010. "NExpectation." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NExpectation.html.
APA
Wolfram 语言. (2010). NExpectation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NExpectation.html 年
BibTeX
@misc{reference.wolfram_2025_nexpectation, author="Wolfram Research", title="{NExpectation}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/NExpectation.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_nexpectation, organization={Wolfram Research}, title={NExpectation}, year={2010}, url={https://reference.wolfram.com/language/ref/NExpectation.html}, note=[Accessed: 08-January-2026]}