NonlinearStateSpaceModel
NonlinearStateSpaceModel[{f,g},x,u]
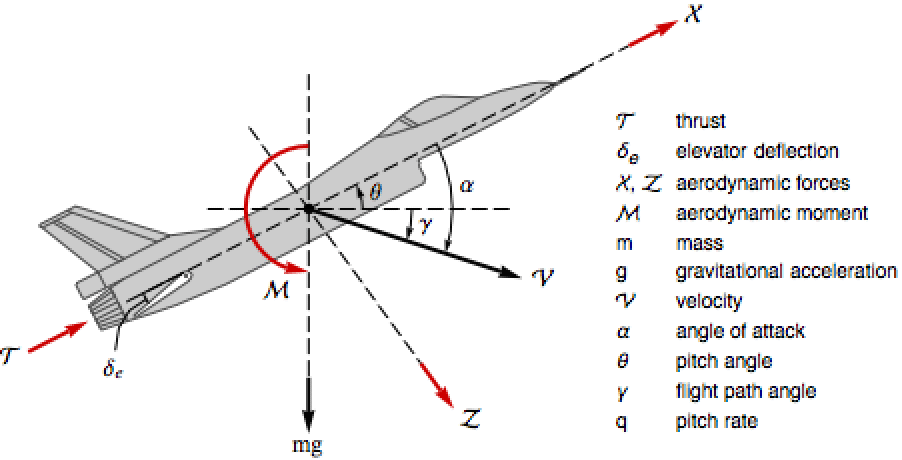
モデル ![]() ,
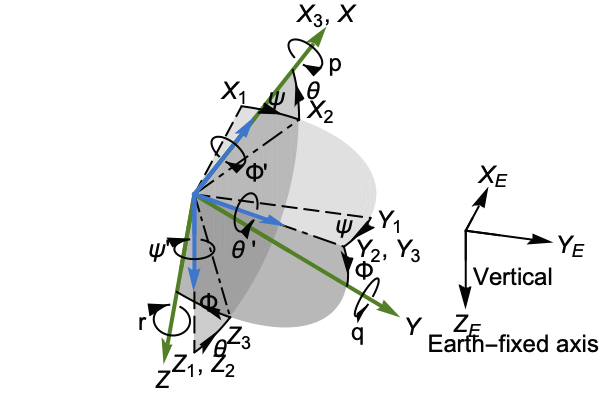
, ![]() を表す.
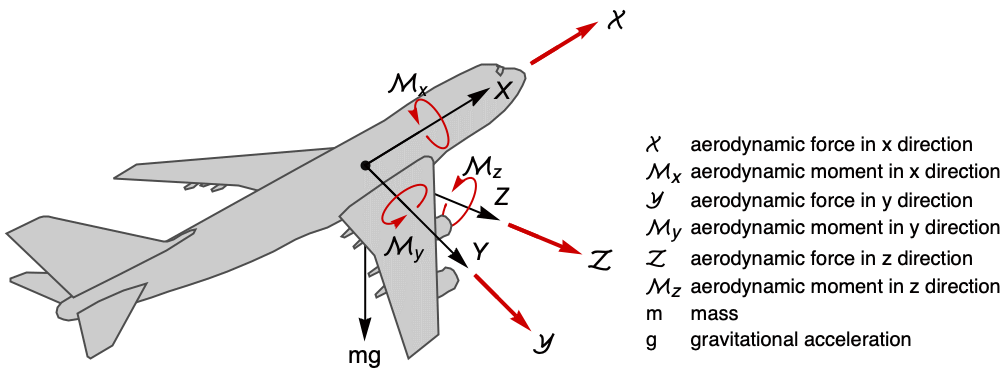
を表す.
系のモデル sys に対応する状態空間表現を与える.
NonlinearStateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},t]
従属変数 xi,入力変数 ui,操作値 xi0 および ui0,出力 gi,独立変数 t である微分方程式 eqns の,状態空間モデルを与える.
詳細とオプション

- NonlinearStateSpaceModelは,状態空間モデルの一般化された表現である.
- NonlinearStateSpaceModel[{f},x,u]は
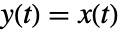 を想定する.
を想定する. - NonlinearStateSpaceModel[{f,g},x,u,y,t]は,明示的に出力変数 y および独立変数 t を指定する.
- NonlinearStateSpaceModelは,状態 x および入力 u についての操作値を使うことができる.
- NonlinearStateSpaceModel[…,{{x1,x10},…},{{u1,u10},…},…]を使って系の操作値を示すことができる.
- NonlinearStateSpaceModel[sys]では,次の系を変換することができる.
-
AffineStateSpaceModel 厳密変換 StateSpaceModel 厳密変換 TransferFunctionModel 厳密変換 - NonlinearStateSpaceModel[eqns,…] では,テイラー(Taylor)の線形化は,微分方程式 eqns の点
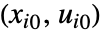 の付近で,
の付近で,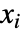 の最高階導関数について行われる.
の最高階導関数について行われる. - 操作点 vi0 がAutomaticの計算では,操作点は通常0であるとみなされる.
- 次のオプションを使うことができる.
-
ExternalTypeSignature Automatic 埋め込まれたコードの変数型 SamplingPeriod Automatic サンプリング周期 SystemsModelLabels Automatic 変数のラベル - NonlinearStateSpaceModelは,OutputResponse,SystemsModelSeriesConnect等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (18)
基本的な用法 (5)
他を0にホールドしつつ,各入力チャンネルに適用された単位ステップへの応答:
操作値付近での線形化を使ってStateSpaceModelを得る:
系の変換 (4)
指定された状態のStateSpaceModelの非線形表現:
デフォルト状態のTransferFunctionModelの非線形状態空間表現:
状態を保存してのAffineStateSpaceModelの非線形表現:
モデル操作 (3)
操作値 (6)
SystemsModelDeleteを使って削除された状態と入力は,その操作値に設定される:
SystemsModelExtractによって抽出されたのではない状態と入力も同様である:
StateSpaceTransformは,古い状態の値が指定されている場合は,新たな状態の操作値を計算する:
デフォルトで,シミュレーション関数は相幸を初期値として仮定する:
StateSpaceModelは,すべての操作値について初期化する:
AffineStateSpaceModelは入力変数の操作値についてのみ初期化する:
NonlinearStateSpaceModelは,常微分方程式に沿って指定された操作値を保存する:
FullInformationOutputRegulatorは,ゲイン ![]() を計算するために,操作値について初期化する:
を計算するために,操作値について初期化する:
アプリケーション (5)
化学系 (2)
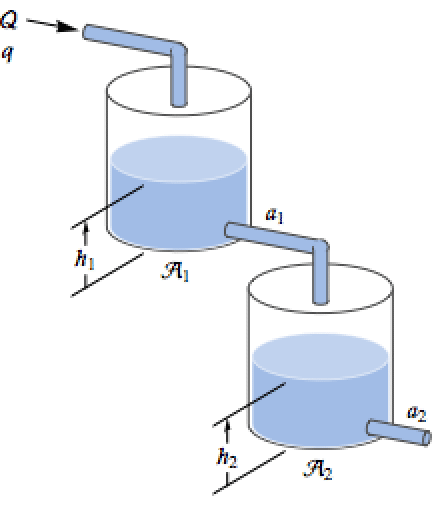
NonlinearStateSpaceModelを使って2槽系の方程式を指定し,この系のシミュレーションを行う:
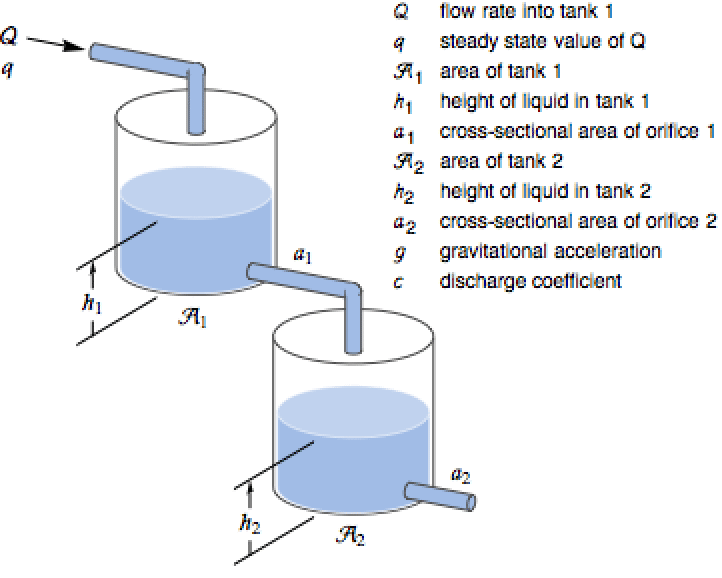
ベルヌーイ(Bernoulli)の法則および質量平衡を使って,結果の微分方程式を導出する:
流量についてのより高い定常状態値では層のレベルはより高くなる:
線形化モデルおよびPIDTuneを使ってPID制御器を得る:
航空宇宙系 (2)
拡張カルマンフィルタ (1)
車輪付きロボットの動きを追跡する,拡張カルマンフィルタを設計する:
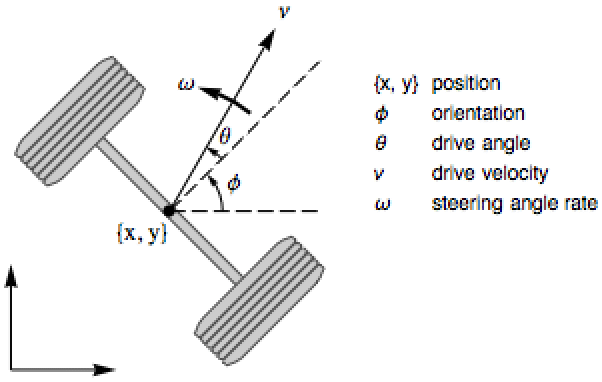
NonlinearStateSpaceModelを使って推定器を組み立てる:
初期位置![]() および一連の入力からロボットのソミュレーションを行う:
および一連の入力からロボットのソミュレーションを行う:
系への入力と雑音の多い測度を使って,フィルタの応答のシミュレーションを行う:
特性と関係 (3)
入力を線形化することでNonlinearStateSpaceModelをAffineStateSpaceModelに変換する:
状態および入力を線形化することでNonlinearStateSpaceModelをStateSpaceModelに変換する:
状態および入力を線形化することでTransferFunctionModelに変換する:
テキスト
Wolfram Research (2014), NonlinearStateSpaceModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html.
CMS
Wolfram Language. 2014. "NonlinearStateSpaceModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html.
APA
Wolfram Language. (2014). NonlinearStateSpaceModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html