NonlinearStateSpaceModel
NonlinearStateSpaceModel[{f,g},x,u]
表示模型 ![]() ,
, ![]() .
.
给出对应于系统模型 sys 的状态-空间表示.
NonlinearStateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},t]
给出微分方程 eqns 的状态-空间模型,方程含有因变量 xi,输入变量 ui,工作值 xi0 和 ui0,输出 gi 和自变量 t.
更多信息和选项

- NonlinearStateSpaceModel 为状态-空间模型的通用表示形式.
- NonlinearStateSpaceModel[{f},x,u] 假设
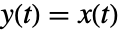 .
. - NonlinearStateSpaceModel[{f,g},x,u,y,t] 明确指定输出变量 y 和自变量 t.
- NonlinearStateSpaceModel 允许为状态 x 和输入 u 设定工作值.
- NonlinearStateSpaceModel[…,{{x1,x10},…},{{u1,u10},…},…] 用来表明系统的工作值.
- 在 NonlinearStateSpaceModel[sys] 中,可以转换下述系统:
-
AffineStateSpaceModel 精确转换 StateSpaceModel 精确转换 TransferFunctionModel 精确转换 - 在 NonlinearStateSpaceModel[eqns,…] 中,泰勒线性化是关于
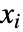 在微分方程 eqns 的点
在微分方程 eqns 的点 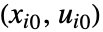 处的最高阶导数做线性化.
处的最高阶导数做线性化. - 在将工作点 vi0 设为 Automatic 的计算中,通常假定为0.
- 可以给出下列选项:
-
ExternalTypeSignature Automatic 嵌入代码的变量类型 SamplingPeriod Automatic 采样周期 SystemsModelLabels Automatic 变量的标签 - NonlinearStateSpaceModel 可用在诸如 OutputResponse 和 SystemsModelSeriesConnect 这样的函数中.
范例
打开所有单元关闭所有单元范围 (18)
基本用途 (5)
对其中一个输入通道施加单位阶跃信号,另一个输入为零,系统响应为:
通过关于工作值的线性化,获取 StateSpaceModel:
系统转换 (4)
指定状态下,StateSpaceModel 的非线性表示:
缺省状态下,TransferFunctionModel 的非线性状态-空间表示:
AffineStateSpaceModel 的非线性表示,保存状态:
模型操控 (3)
工作值 (6)
用 SystemsModelDelete 删除掉的状态和输入被设置为工作值:
没有被 SystemsModelExtract 提取的状态和输入也同样被设置为工作值:
如果旧的状态被变换,StateSpaceTransform 会计算新状态的工作值:
StateSpaceModel 将模型关于所有工作值线性化:
AffineStateSpaceModel 只将模型关于输入变量的工作值线性化:
NonlinearStateSpaceModel 保留和 ODE 一起指定的工作值:
FullInformationOutputRegulator 关于工作值线性化来计算增益 ![]() :
:
应用 (5)
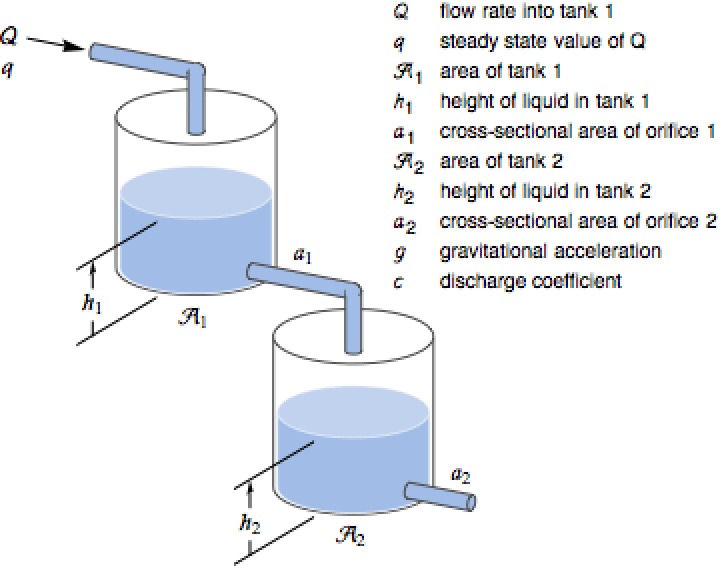
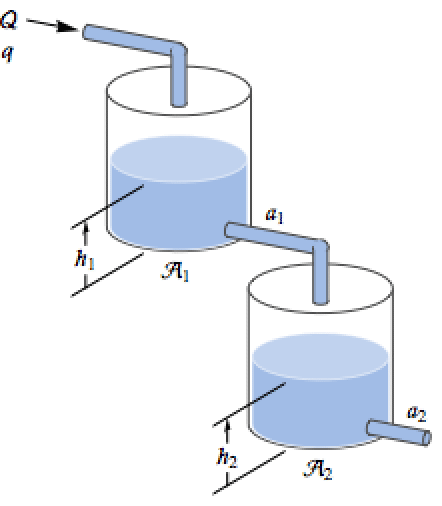
化学系统 (2)
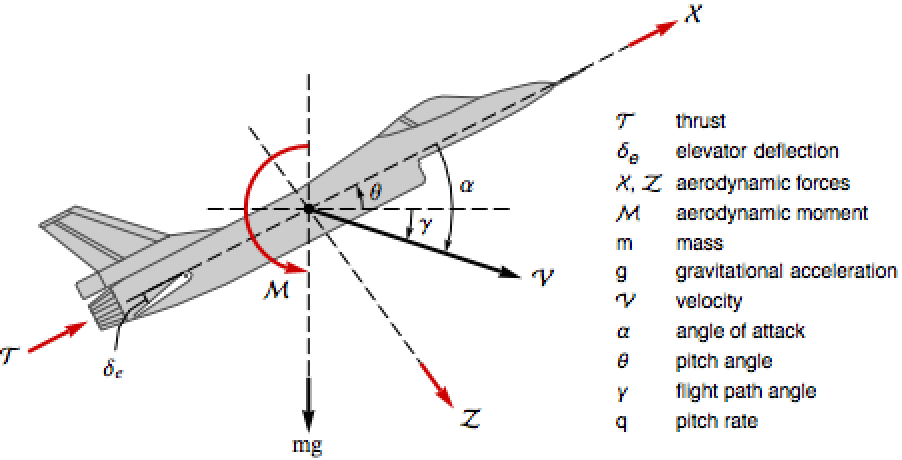
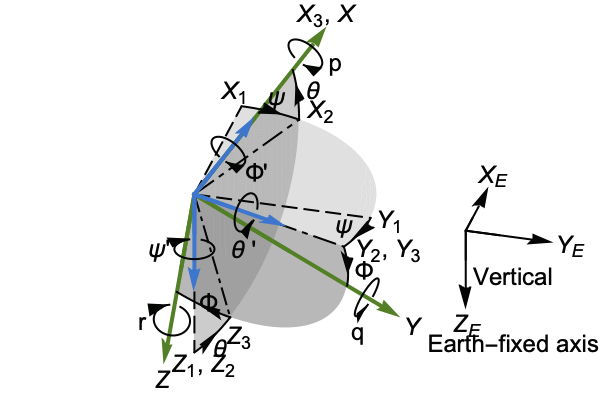
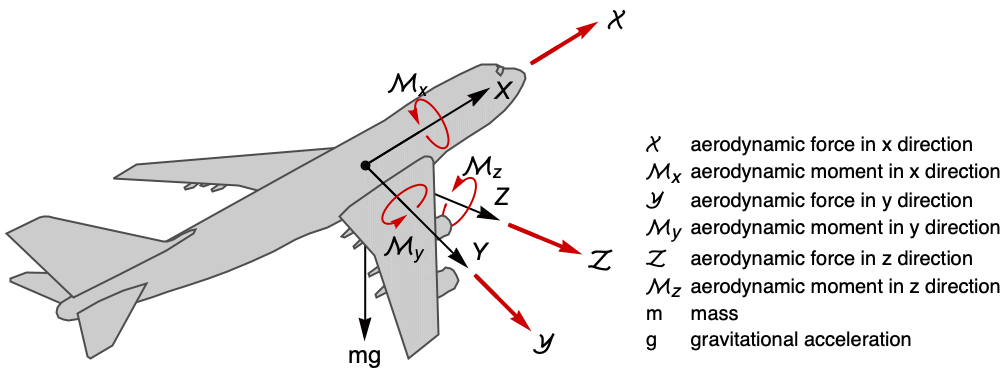
航空航天系统 (2)
扩展卡尔曼滤波器 (1)
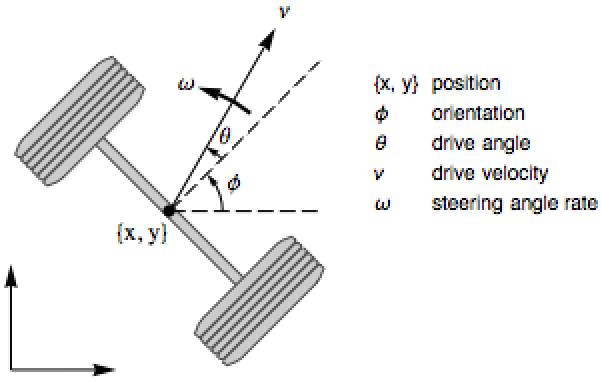
用 NonlinearStateSpaceModel 组成估算器:
属性和关系 (3)
通过对输入做线性化处理,可将 NonlinearStateSpaceModel 转换成 AffineStateSpaceModel:
通过对状态和输入做线性化处理,可将 NonlinearStateSpaceModel 转换成 StateSpaceModel:
通过对状态和输入做线性化处理,还可将其转换成 TransferFunctionModel:
文本
Wolfram Research (2014),NonlinearStateSpaceModel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html.
CMS
Wolfram 语言. 2014. "NonlinearStateSpaceModel." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html.
APA
Wolfram 语言. (2014). NonlinearStateSpaceModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NonlinearStateSpaceModel.html 年