ParetoPickandsDistribution
ParetoPickandsDistribution[μ,σ,ξ]
位置母数 μ,尺度母数 σ,形状母数 ξ のパレート(Pareto)・ピカンズ(Pickands)分布を与える.
位置母数が0で単位尺度母数を持つ標準パレート・ピカンズ分布を与える.
詳細

- ParetoPickandsDistributionは一般化パレート分布(GPD)としても知られている.
- ParetoPickandsDistributionの σ は任意の正の実数でよく,μ と ξ は任意の実数でよい.
- 一般化パレート分布における値
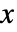 についての確率密度関数は,
についての確率密度関数は,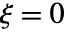 かつ
かつ 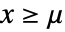 のときは
のときは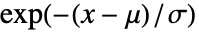 に比例し,
に比例し,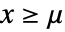 かつ
かつ 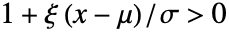 で
で 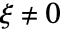 のときは
のときは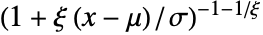 に比例する. »
に比例する. » - 一般化パレート分布における値
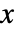 の生存時間関数は,
の生存時間関数は,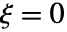 かつ
かつ 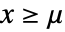 のときは
のときは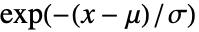 に等しく,
に等しく,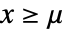 かつ
かつ 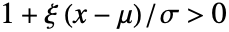 で
で 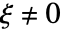 のときは
のときは 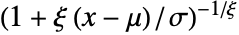 に等しい.
に等しい. - 一般化パレート分布における値
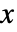 のハザード関数は,
のハザード関数は,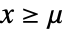 かつ
かつ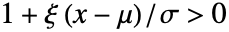 のときは
のときは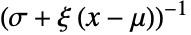 に等しく,その他の場合は0である. »
に等しく,その他の場合は0である. » - ParetoPickandsDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる.
例題
すべて開くすべて閉じる例 (4)
スコープ (7)
データのヒストグラムを母集団のPDFと比較する:
一般化パレート分布の歪度は,定義されているところで ξ のみに依存する:
パレート・ピカンズ分布の尖度は,定義されているところで形状母数のみに依存する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (2)
StudentTDistributionのようなベキ裾分布の裾をモデル化する:
大きい方から ![]() 番目の要素を0にシフトして,サンプルの大きい方から
番目の要素を0にシフトして,サンプルの大きい方から ![]() 個の要素を抽出する関数を定義する:
個の要素を抽出する関数を定義する:
特性と関係 (8)
パレート・ピカンズ分布族は左切断(閾値安定性)の下で閉じている:
切断点がParetoPickandsDistributionの台に属すると仮定して,結果をRefine(簡約)する:
![]() のパレート・ピカンズ分布はUniformDistributionに等しい:
のパレート・ピカンズ分布はUniformDistributionに等しい:
![]() のパレート・ピカンズ分布はシフトされたExponentialDistributionに等しい:
のパレート・ピカンズ分布はシフトされたExponentialDistributionに等しい:
パレート・ピカンズ分布族はタイプIおよびタイプIIのParetoDistributionを含む:
正の形状母数 ξ を持つ標準パレート・ピカンズ分布はTsallisQExponentialDistributionの特殊ケースである:
標準パレート・ピカンズ分布は確率的に順序付けられている.つまり,任意の2つのパラメータ ![]() について,累積分布関数もまたすべての
について,累積分布関数もまたすべての ![]() について(逆)順序に
について(逆)順序に ![]() なっている :
なっている :
正の形状母数 ξ を持つパレート・ピカンズ分布は,比率がGammaDistributionに従うExponentialDistributionの母数混合として出現する:
テキスト
Wolfram Research (2019), ParetoPickandsDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
CMS
Wolfram Language. 2019. "ParetoPickandsDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
APA
Wolfram Language. (2019). ParetoPickandsDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html