TsallisQExponentialDistribution[λ,q]
represents a Tsallis ![]() -exponential distribution with scale inversely proportional to parameter λ.
-exponential distribution with scale inversely proportional to parameter λ.


TsallisQExponentialDistribution
TsallisQExponentialDistribution[λ,q]
represents a Tsallis ![]() -exponential distribution with scale inversely proportional to parameter λ.
-exponential distribution with scale inversely proportional to parameter λ.
Details
- The probability density for value
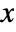 in a Tsallis
in a Tsallis 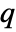 -exponential distribution is proportional to
-exponential distribution is proportional to 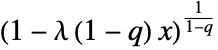 for
for 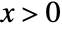 , and is zero for
, and is zero for 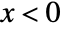 .
. - TsallisQExponentialDistribution allows λ to be any positive real number and
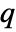 to be any real number such that
to be any real number such that 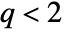 .
. - TsallisQExponentialDistribution allows λ to be a quantity of any unit dimension, and q to be a dimensionless quantity. »
- TsallisQExponentialDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- TsallisQExponentialDistribution[λ,q] represents a continuous statistical distribution supported over the interval
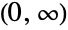 and parametrized by a positive real number λ (called a "scale parameter") and by a real number
and parametrized by a positive real number λ (called a "scale parameter") and by a real number 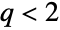 , which together determine the overall behavior of its probability density function (PDF). Depending on the values of λ and
, which together determine the overall behavior of its probability density function (PDF). Depending on the values of λ and 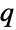 , the PDF of a Tsallis
, the PDF of a Tsallis 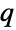 -exponential distribution may have any of a number of shapes, including unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with potential singularities approaching the lower boundary of its domain. In addition, the tails of the PDF are typically "fat" (i.e. the PDF decreases non-exponentially for large values
-exponential distribution may have any of a number of shapes, including unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with potential singularities approaching the lower boundary of its domain. In addition, the tails of the PDF are typically "fat" (i.e. the PDF decreases non-exponentially for large values 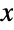 ) but are "thin" (i.e. the PDF decreases exponentially for large
) but are "thin" (i.e. the PDF decreases exponentially for large 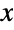 ) when
) when 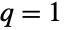 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Tsallis
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Tsallis 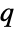 -exponential distribution is often referred to merely as the
-exponential distribution is often referred to merely as the 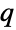 -exponential distribution.
-exponential distribution. - The Tsallis
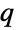 -exponential distribution is named for Brazilian physicist Constantino Tsallis and is derived via maximization of the so-called Tsallis entropy (in statistical mechanics) subject to certain conditions. Along with the related
-exponential distribution is named for Brazilian physicist Constantino Tsallis and is derived via maximization of the so-called Tsallis entropy (in statistical mechanics) subject to certain conditions. Along with the related 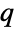 -Gaussian distribution, the
-Gaussian distribution, the 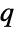 -exponential distribution is one of a family of probability distributions referred to collectively as Tsallis distributions and derived according to the above-mentioned process. The
-exponential distribution is one of a family of probability distributions referred to collectively as Tsallis distributions and derived according to the above-mentioned process. The 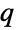 -exponential distribution is becoming increasingly more utilized across various subfields of physics and has also been used to model phenomena like wealth distribution and asset pricing in fields such as economics, finance, and actuarial science.
-exponential distribution is becoming increasingly more utilized across various subfields of physics and has also been used to model phenomena like wealth distribution and asset pricing in fields such as economics, finance, and actuarial science. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a
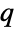 -exponential distribution. Distributed[x,TsallisQExponentialDistribution[λ,q]], written more concisely as xTsallisQExponentialDistribution[λ,q], can be used to assert that a random variable x is distributed according to a
-exponential distribution. Distributed[x,TsallisQExponentialDistribution[λ,q]], written more concisely as xTsallisQExponentialDistribution[λ,q], can be used to assert that a random variable x is distributed according to a 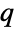 -exponential distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
-exponential distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation. - The probability density and cumulative distribution functions for
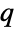 -exponential distributions may be given using PDF[TsallisQExponentialDistribution[λ,q],x] and CDF[TsallisQExponentialDistribution[λ,q],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
-exponential distributions may be given using PDF[TsallisQExponentialDistribution[λ,q],x] and CDF[TsallisQExponentialDistribution[λ,q],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. - DistributionFitTest can be used to test if a given dataset is consistent with a
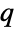 -exponential distribution, EstimatedDistribution to estimate a parametric
-exponential distribution, EstimatedDistribution to estimate a parametric 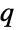 -exponential distribution from given data, and FindDistributionParameters to fit data to a
-exponential distribution from given data, and FindDistributionParameters to fit data to a 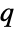 -exponential distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic
-exponential distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic 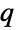 -exponential distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic
-exponential distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic 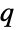 -exponential distribution.
-exponential distribution. - TransformedDistribution can be used to represent a transformed
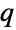 -exponential distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a
-exponential distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a 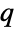 -exponential distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving
-exponential distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving 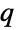 -exponential distributions.
-exponential distributions. - TsallisQExponentialDistribution is related to a number of other distributions. TsallisQExponentialDistribution is an immediate generalization of ExponentialDistribution, in the sense that the PDF of TsallisQExponentialDistribution[λ,1] is precisely the same as that of ExponentialDistribution[λ]. For different values of
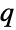 , TsallisQExponentialDistribution may be viewed either as a special case of ParetoDistribution (for
, TsallisQExponentialDistribution may be viewed either as a special case of ParetoDistribution (for 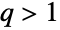 ) or as a limiting case of PERTDistribution (for
) or as a limiting case of PERTDistribution (for 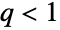 ). For
). For 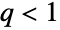 , TsallisQExponentialDistribution is a transformation (TransformedDistribution) of BetaDistribution, while for general
, TsallisQExponentialDistribution is a transformation (TransformedDistribution) of BetaDistribution, while for general 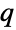 , TsallisQExponentialDistribution is also closely related to TsallisQGaussianDistribution, NormalDistribution, and WeibullDistribution.
, TsallisQExponentialDistribution is also closely related to TsallisQGaussianDistribution, NormalDistribution, and WeibullDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a ![]() -exponential distribution:
-exponential distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (4)
A battery has a lifespan that is ![]() -exponentially distributed with parameters
-exponentially distributed with parameters ![]() per hour and
per hour and ![]() . Find the probability that a random battery has a lifespan of less than 2500 hours:
. Find the probability that a random battery has a lifespan of less than 2500 hours:
Compute directly using the CDF:
A product has a time to failure that is ![]() -exponentially distributed with parameters
-exponentially distributed with parameters ![]() and
and ![]() . Find the reliability of the product at 1, 2, and 3 years:
. Find the reliability of the product at 1, 2, and 3 years:
Find the failure rate of the product at 1, 2, and 3 years:
Suppose the lifetime of an appliance has a ![]() -exponential distribution with parameter
-exponential distribution with parameter ![]() and an average lifetime of 10 years. Find the appliance lifetime distribution:
and an average lifetime of 10 years. Find the appliance lifetime distribution:
Find the probability that a used appliance with ![]() years of use will not fail in the next 5 years:
years of use will not fail in the next 5 years:
The waiting time in a restaurant is ![]() -exponentially distributed with parameter
-exponentially distributed with parameter ![]() and an average wait time of 5 minutes. Find the probability that the customer will have to wait more than 10 minutes:
and an average wait time of 5 minutes. Find the probability that the customer will have to wait more than 10 minutes:
Find the probability that the customer has to wait an additional 10 minutes, given that he or she has already been waiting for at least 10 minutes:
Properties & Relations (7)
Tsallis ![]() -exponential distribution is closed under scaling by a positive factor:
-exponential distribution is closed under scaling by a positive factor:
Tsallis ![]() -exponential distribution has unbounded support for
-exponential distribution has unbounded support for ![]() :
:
Relationships to other distributions:
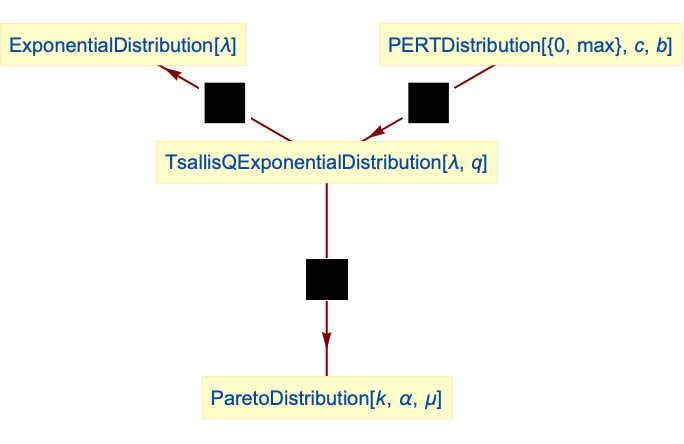
Tsallis ![]() -exponential distribution simplifies to the exponential distribution:
-exponential distribution simplifies to the exponential distribution:
Tsallis ![]() -exponential distribution is equivalent to a Pareto distribution for
-exponential distribution is equivalent to a Pareto distribution for ![]() :
:
Tsallis ![]() -exponential distribution for
-exponential distribution for ![]() is a limiting case of PERTDistribution:
is a limiting case of PERTDistribution:
Tsallis ![]() -exponential distribution for
-exponential distribution for ![]() is a transformed BetaDistribution:
is a transformed BetaDistribution:
Possible Issues (2)
TsallisQExponentialDistribution is not defined when λ is not a positive real number or when ![]() is not a positive real number:
is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Related Guides
Text
Wolfram Research (2012), TsallisQExponentialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TsallisQExponentialDistribution.html (updated 2016).
CMS
Wolfram Language. 2012. "TsallisQExponentialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/TsallisQExponentialDistribution.html.
APA
Wolfram Language. (2012). TsallisQExponentialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TsallisQExponentialDistribution.html
BibTeX
@misc{reference.wolfram_2025_tsallisqexponentialdistribution, author="Wolfram Research", title="{TsallisQExponentialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/TsallisQExponentialDistribution.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_tsallisqexponentialdistribution, organization={Wolfram Research}, title={TsallisQExponentialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/TsallisQExponentialDistribution.html}, note=[Accessed: 14-January-2026]}