ParetoPickandsDistribution[μ,σ,ξ]
gives a Pareto–Pickands distribution with location parameter μ, scale parameter σ and shape parameter ξ.
gives the standard Pareto–Pickands distribution with zero location and unit scale parameters.


ParetoPickandsDistribution
ParetoPickandsDistribution[μ,σ,ξ]
gives a Pareto–Pickands distribution with location parameter μ, scale parameter σ and shape parameter ξ.
gives the standard Pareto–Pickands distribution with zero location and unit scale parameters.
Details

- The ParetoPickandsDistribution is also known as generalized Pareto distribution or GPD.
- ParetoPickandsDistribution allows σ to be any positive real number and μ and ξ to be any real numbers.
- The probability density function for value
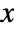 in the generalized Pareto distribution is proportional to
in the generalized Pareto distribution is proportional to 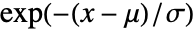 for
for 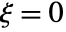 and
and 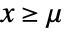 , and
, and 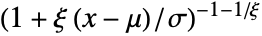 for
for 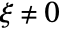 for
for 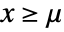 and
and 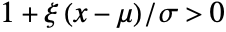 . »
. » - The survival function for value
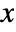 in the generalized Pareto distribution equals
in the generalized Pareto distribution equals 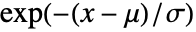 for
for 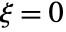 and
and 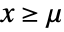 , and
, and 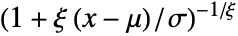 for
for 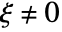 for
for 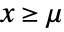 and
and 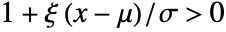 .
. - The hazard function for value
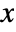 in the generalized Pareto distribution equals
in the generalized Pareto distribution equals 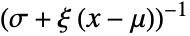 for
for 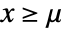 and
and 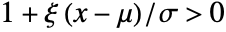 , and zero otherwise. »
, and zero otherwise. » - ParetoPickandsDistribution can be used with such functions as Mean, CDF and RandomVariate.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from generalized Pareto distribution:
Compare data histogram to the population PDF:
Generate a sample of pseudorandom numbers from generalized Pareto distribution:
Estimate the distribution parameters from sample data:
Compare sample histogram with probability density functions of the estimated distribution:
Skewness of the generalized Pareto distribution depends only on ξ where defined:
Invert skewness as a function of the shape parameter ξ:
Visualize the inverse function:
Kurtosis of Pareto–Pickands distribution only depends on the shape parameter where defined:
The minimal value of the kurtosis within the family of Pareto–Pickands distributions:
Table of moments of Pareto–Pickands distribution:
Closed form for symbolic order:
Closed form for symbolic order:
Quantile function of Pareto–Pickands distribution:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
Model a tail of a power‐tail distribution, e.g. StudentTDistribution:
Truncate data to the left at ![]() :
:
Fit truncated data to Pareto–Pickands distribution:
Generate a sample from standard Gaussian distribution:
Define a function to extract ![]() largest elements of the sample while shifting the
largest elements of the sample while shifting the ![]()
![]() largest element to zero:
largest element to zero:
Exceedance in large data samples is well described by Pareto–Pickands family of distributions:
Illustrate this fact with a sequence of probability plots of exceedance data against Pareto–Pickands family of distributions:
Properties & Relations (8)
Pareto–Pickands distribution family is closed under affine transformations:
Pareto–Pickands distribution family is closed under left truncation (threshold stability):
Refine the result, assuming that truncation point belongs to the support of ParetoPickandsDistribution:
Pareto–Pickands distribution with ![]() is equivalent to a UniformDistribution:
is equivalent to a UniformDistribution:
Pareto–Pickands distribution with ![]() is equivalent to a shifted ExponentialDistribution:
is equivalent to a shifted ExponentialDistribution:
The Pareto–Pickands distribution family includes ParetoDistribution of types I and II:
Check that probability density functions coincide:
Standard Pareto–Pickands distribution with a positive shape parameter ξ is a special case of TsallisQExponentialDistribution:
Standard Pareto–Pickands distributions are stochastically ordered, i.e. for any two parameters ![]() , cumulative distributions functions are (reverse) ordered
, cumulative distributions functions are (reverse) ordered ![]() for all
for all ![]() :
:
Pareto–Pickands distribution with positive shape parameter ξ occurs as a parametric mixture of ExponentialDistribution whose rate follows a GammaDistribution:
Related Guides
History
Text
Wolfram Research (2019), ParetoPickandsDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
CMS
Wolfram Language. 2019. "ParetoPickandsDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
APA
Wolfram Language. (2019). ParetoPickandsDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html
BibTeX
@misc{reference.wolfram_2025_paretopickandsdistribution, author="Wolfram Research", title="{ParetoPickandsDistribution}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html}", note=[Accessed: 11-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_paretopickandsdistribution, organization={Wolfram Research}, title={ParetoPickandsDistribution}, year={2019}, url={https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html}, note=[Accessed: 11-December-2025]}