ParetoPickandsDistribution
ParetoPickandsDistribution[μ,σ,ξ]
给出 Pareto–Pickands 分布,其位置参数为 μ,尺度参数为 σ,形状参数为 ξ.
给出位置参数为 0 且尺度参数为 1 的标准 Pareto–Pickands 分布.
更多信息

- ParetoPickandsDistribution 亦称为广义 Pareto 分布或 GPD.
- ParetoPickandsDistribution 允许 σ 为任意正,μ 和 ξ 为任意实数.
- 如果
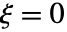 且
且 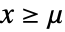 ,广义 Pareto 分布中的值
,广义 Pareto 分布中的值 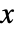 的概率密度函数与
的概率密度函数与 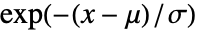 成正比,如果
成正比,如果 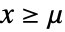 且
且 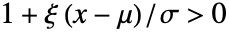 时
时 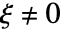 ,则与
,则与 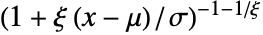 成正比. »
成正比. » - 如果
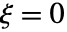 且
且 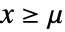 ,广义 Pareto 分布中的值
,广义 Pareto 分布中的值 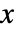 的存活函数为
的存活函数为 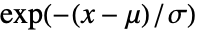 ,如果
,如果 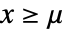 且
且 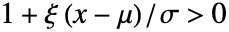 时
时 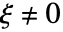 ,则为
,则为 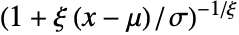 .
. - 如果
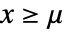 且
且 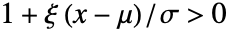 ,广义 Pareto 分布中的值
,广义 Pareto 分布中的值 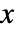 的风险函数等于
的风险函数等于 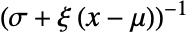 ,否则等于零. »
,否则等于零. » - ParetoPickandsDistribution 可与 Mean、CDF 和 RandomVariate 等函数一起使用.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (7)
将数据的直方图与总体的 PDF 进行比较:
广义 Pareto–Pickands 分布的峰度只取决于有定义处的形状参数:
参数中对 Quantity 使用的一致性产生了 QuantityDistribution:
应用 (2)
模拟一个重尾分布的尾部,如 StudentTDistribution:
定义一个函数来提取样本的 ![]() 个最大的元素,同时将第
个最大的元素,同时将第 ![]() 个最大的元素移位至零:
个最大的元素移位至零:
属性和关系 (8)
Pareto–Pickands 系列分布在经过仿射变换后依然是 Pareto–Pickands 分布:
Pareto–Pickands 分布系列在左截尾的情况下是依然是 Pareto–Pickands 分布(阈值稳定性):
Refine 结果,假定截断点属于 ParetoPickandsDistribution:
![]() 时 Pareto–Pickands 分布等价于 UniformDistribution:
时 Pareto–Pickands 分布等价于 UniformDistribution:
![]() 时 Pareto–Pickands 分布等价于经过位移的 ExponentialDistribution:
时 Pareto–Pickands 分布等价于经过位移的 ExponentialDistribution:
Pareto–Pickands 分布系列包括 I 型和 II 型 ParetoDistribution:
具有正的形状参数 ξ 的标准 Pareto–Pickands 分布是 TsallisQExponentialDistribution 的特例:
标准帕累托 Pickands 分布是随机有序的,即对于任意两个参数 ![]() ,累积分布函数对于所有
,累积分布函数对于所有 ![]() 是(反向)排序为
是(反向)排序为 ![]() :
:
具有正的形状参数 ξ 的 Pareto–Pickands 分布可由 ExponentialDistribution (其率参数服从 GammaDistribution)经参数混合而得:
文本
Wolfram Research (2019),ParetoPickandsDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
CMS
Wolfram 语言. 2019. "ParetoPickandsDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html.
APA
Wolfram 语言. (2019). ParetoPickandsDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ParetoPickandsDistribution.html 年