PolarCurve

PolarCurve[r,{θ,θmin,θmax}]

gives a polar curve with radius r as a function of angle θ.

Details

  • PolarCurve is also known as polar graph.
  • PolarCurve is typically used to describe a geometric region inherently tied to direction and length from a center point.
  • PolarCurve[r,{θ,θmin,θmax}] gives a parametric curve with 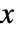-position 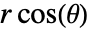and 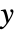-position 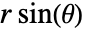corresponding to , .
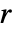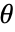  • PolarCurve[r,θ] is effectively equivalent to PolarCurve[r,{θ,0,2π}].
  • PolarCurve is a geometric region and can be used in functions such as ArcLength, Reduce and Integrate.

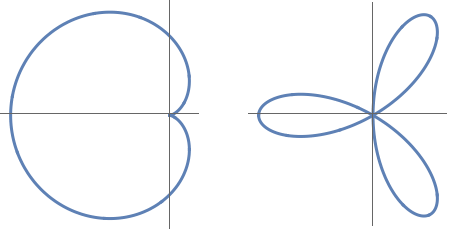
Examples

open allclose all

Basic Examples  (1)

Specify a polar curve:

Scope  (2)

Polar curve with a radius:

Embedding dimension:

Geometric dimension:

Arc length:

Properties & Relations  (2)

Use PolarPlot to plot a polar curve:

Use RegionConvert to convert a polar curve to the parametric form:

Wolfram Research (2024), PolarCurve, Wolfram Language function, https://reference.wolfram.com/language/ref/PolarCurve.html.

Text

Wolfram Research (2024), PolarCurve, Wolfram Language function, https://reference.wolfram.com/language/ref/PolarCurve.html.

CMS

Wolfram Language. 2024. "PolarCurve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PolarCurve.html.

APA

Wolfram Language. (2024). PolarCurve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolarCurve.html

BibTeX

@misc{reference.wolfram_2025_polarcurve, author="Wolfram Research", title="{PolarCurve}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PolarCurve.html}", note=[Accessed: 19-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_polarcurve, organization={Wolfram Research}, title={PolarCurve}, year={2024}, url={https://reference.wolfram.com/language/ref/PolarCurve.html}, note=[Accessed: 19-March-2025 ]}