PowerExpand

PowerExpand[expr]

すべての積のベキとベキを展開する．

PowerExpand[expr,{x1,x2,…}]

変数 xi についてのみ展開する．

詳細とオプション

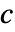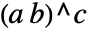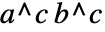  • PowerExpandは， の形式にかかわらず を に変換する．
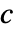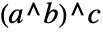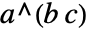  • PowerExpandは，また， の形式にかかわらず を に変換する．
  • PowerExpandによってなされる変換は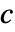， が整数または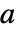， と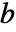 が正の実数であるときに限って，一般に正しいといえる．
  • PowerExpandはLog[a^b]をb Log[a]に変換する．
  • PowerExpandは一般に多価関数の分岐問題は無視するので，式の数値は保たれないことがある．
  • PowerExpandは自動的に，リスト，方程式，不等式，論理関数に縫い込まれる．
  • PowerExpandには，使用する仮定を指定するオプションAssumptionsがある．
  • Assumptionsオプションのデフォルトの設定値はAutomaticで，仮定の最大集合に相当する．
  • Assumptionsassum のとき，PowerExpandが行う変換は仮定 assum が満足される場合は常に正しい．
  • Assumptions:>$Assumptionsのときは，Assumingを使ってPowerExpandのデフォルトの仮定を指定することができる．

例題

すべて開くすべて閉じる

例  (1)

暗示的に正の実数を想定して平方根を展開する：

PowerExpandなしでは展開できない：

展開は正の実変数についてのみ正しい：

次は完全に正しい解を与える：

次は，指定の仮定に基づいた場合は正しい結果を与える：

スコープ  (11)

積のベキを展開する．結果はすべてにおいて正しい訳ではないかもしれない：

積のベキを展開する一般的な公式：

ネストしたベキを展開する．結果はすべてにおいて正しい訳ではないかもしれない：

ネストしたベキを展開する一般的な公式：

ベキの対数を展開する．結果はすべてにおいて正しい訳ではないかもしれない：

ベキの対数を展開する一般的な公式：

積の対数を展開する．結果はすべてにおいて正しい訳ではないかもしれない：

積の対数を展開する一般的な公式：

逆三角関数と三角関数の組合せを展開する：

次は，普遍的に正しい公式を返す：

指定の仮定の下で有効な展開を計算する：

積の引数を展開する：

aとbについてのみ展開する：

オプション  (3)

Assumptions  (3)

デフォルト設定のAssumptions -> Automaticでは，展開が常に正しいとは限らない：

仮定が指定されると，その仮定の下で正しい結果が返される：

Assumptions->Trueとすると，PowerExpandは普遍的に正しい展開公式を返す：

アプリケーション  (2)

普遍的に正しい展開規則を求める：

指定の仮定の下で展開する：

特性と関係  (5)

PowerExpandは，指定の仮定の下で有効な展開を行う：

Assumptions->Trueとすると，PowerExpandは一般的な展開公式を返す：

RefineとSimplifyは指定の仮定の下で有効な展開を行う：

FunctionExpandを使ってを別の方法で表す：

PiecewiseExpandを使って結果を区分関数として表す：

考えられる問題  (1)

Assumptions->AutomaticとしたPowerExpandが返す結果は正しくないことがある：

Wolfram Research (1991), PowerExpand, Wolfram言語関数， https://reference.wolfram.com/language/ref/PowerExpand.html （2007年に更新）.

テキスト

Wolfram Research (1991), PowerExpand, Wolfram言語関数， https://reference.wolfram.com/language/ref/PowerExpand.html （2007年に更新）.

CMS

Wolfram Language. 1991. "PowerExpand." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/PowerExpand.html.

APA

Wolfram Language. (1991). PowerExpand. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerExpand.html

BibTeX

@misc{reference.wolfram_2024_powerexpand, author="Wolfram Research", title="{PowerExpand}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/PowerExpand.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_powerexpand, organization={Wolfram Research}, title={PowerExpand}, year={2007}, url={https://reference.wolfram.com/language/ref/PowerExpand.html}, note=[Accessed: 21-November-2024 ]}