PowerSpectralDensity

PowerSpectralDensity[data,ω]

data のパワースペクトル密度を推定する．

PowerSpectralDensity[data,ω,sspec]

data のパワースペクトル密度を平滑化指定 sspec で推定する．

PowerSpectralDensity[tproc,ω]

時系列過程 tproc のパワースペクトル密度を表す．

詳細とオプション

  • PowerSpectralDensityはエネルギースペクトル密度としても知られている．
  • PowerSpectralDensity[tproc,ω]は弱定常時系列過程について 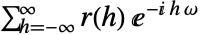として定義される．ただし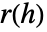，はCovarianceFunction[proc,i]を意味する．
  • 次の平滑化指定 sspec を与えることができる．
  • c切捨てとして c を使う
    w窓関数 w を使う
    {c,w}切捨てと窓関数の両方を使う
  • 窓関数 w および正の整数 c について，PowerSpectralDensity[data,ω,{c,w}]は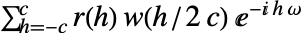として計算される．ただし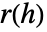，はCovarianceFunction[data,i]として定義される．
  • デフォルトで，切捨て c は 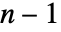になるように選ばれる．ただし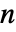， は data の長さであり窓関数はDirichletWindowである．
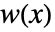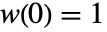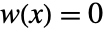  • HammingWindowやParzenWindow等の一般的な窓を含む窓関数 は，TemplateBox[{x}, Abs]>1/2について ，TemplateBox[{{w, (, x, )}}, Abs]<=1，の偶関数である．
  • 窓関数は値のリスト{w1,…}として与えることができる．ただし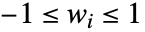，であり，ベクトルの場合には対称的に適用される．
  • PowerSpectralDensityはFourierParametersオプションを取る．次はFourierParametersのよく使われる設定である．
  • {1,1}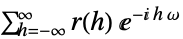デフォルト設定
    {-1,1}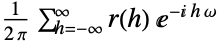しばしば時系列に使われる
    {a,b}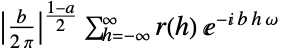一般的な設定

例題

すべて開くすべて閉じる

例  (3)

データのパワースペクトル密度を推定する：

一変量時系列のパワースペクトル密度を計算する：

自己回帰時系列のランダムサンプルについてのサンプルパワースペクトル密度：

切捨てを使ってパワースペクトル密度を計算する：

スコープ  (14)

経験的推定  (4)

一変量時系列についてのパワースペクトル密度を推定する：

ベクトル時系列についてのパワースペクトル密度：

各成分についてのパワースペクトル密度：

成分間の相互パワースペクトル密度：

経路の集合についてパワースペクトル密度を推定する：

経験的パワースペクトル密度関数と理論的なそれとを比較する：

平滑化  (5)

5での切捨てを使って平滑化された推定を得る：

平滑化されたスペクトルをもとのスペクトルと比較する：

NuttallWindowを使ってパワースペクトル密度を計算する：

平滑化されたスペクトルをもとのスペクトルと比較する：

純関数を使って窓を定義する：

平滑化されたスペクトルをもとのスペクトルと比較する：

指定された窓関数の値を使ってパワースペクトル密度を推定する：

明示的なTukeyWindowを持つパワースペクトル密度と比較する：

平滑化されたスペクトルをもとのスペクトルと比較する：

与えられた切捨てと窓関数でパワースペクトル密度を計算する：

平滑化されたスペクトルをもとのスペクトルと比較する：

ランダム過程  (5)

ARProcessについてのパワースペクトル密度：

ベクトルARProcess：

相互スペクトル密度：

MAProcessについてのパワースペクトル密度：

ベクトルMAProcess：

相互スペクトル密度：

ARProcessについてのパワースペクト密度：

ベクトルARMAProcess：

相互スペクトル密度：

実数和分時系列のパワースペクトル密度：

ベクトルFARIMAProcess：

相互スペクトル密度：

季節時系列のパワースペクトル密度：

ベクトルSARMAProcess：

相互スペクトル密度：

オプション  (2)

FourierParametersのデフォルト値：

FourierParametersを変える：

これはスケールされたデフォルト値である：

アプリケーション  (1)

時系列過程の推定にパワースペクトル密度を使う：

平滑化窓を使う：

特性と関係  (11)

時系列のパワースペクトル密度はCovarianceFunctionを変換したものである：

FourierSequenceTransformを使う：

パワースペクトルと比較する：

ベクトル時系列について：

データのパワースペクトル密度は，サンプルCovarianceFunctionを変換したものである：

ListFourierSequenceTransformを適用する：

SamplePowerSpectralDensityと比較する：

ベクトル値時系列について：

ホワイトノイズのパワースペクトル：

MAProcessの特殊ケースと比較する：

積分して分散を求める：

時系列の分散と比較する：

積分してサンプル二次モーメントを求める：

サンプル二次モーメントと比較する：

調和振動数のパワースペクトル密度はPeriodogramArrayに関連している：

PeriodogramArrayと比較する：

零の振動数について：

非零の振動数について：

ベクトルデータについてのパワースペクトル密度の対角要素：

各データ成分について一変量パワースペクトル密度と比較する：

ベクトル過程のパワースペトル密度は0について共役対称である：

一変量過程のパワースペクトル密度は0について対称である：

ベクトル過程のパワースペクトル密度はエルミート行列である：

また，非負の正定値行列である：

サンプル相互スペクトル密度の大きさは成分ごとに与えられる：

サンプルパワースペクトル密度の行列式は，0に等しく一定である：

TransferFunctionModelを使い，時系列のPowerSpectralDensityを計算する：

伝達関数を定義する：

スペクトル密度を計算する：

確かめる：

おもしろい例題  (1)

2つのパワースペクトル密度の積を3Dでプロットする：

Wolfram Research (2012), PowerSpectralDensity, Wolfram言語関数， https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.

テキスト

Wolfram Research (2012), PowerSpectralDensity, Wolfram言語関数， https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.

CMS

Wolfram Language. 2012. "PowerSpectralDensity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.

APA

Wolfram Language. (2012). PowerSpectralDensity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerSpectralDensity.html

BibTeX

@misc{reference.wolfram_2024_powerspectraldensity, author="Wolfram Research", title="{PowerSpectralDensity}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PowerSpectralDensity.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_powerspectraldensity, organization={Wolfram Research}, title={PowerSpectralDensity}, year={2012}, url={https://reference.wolfram.com/language/ref/PowerSpectralDensity.html}, note=[Accessed: 21-November-2024 ]}