PowerSpectralDensity
PowerSpectralDensity[data,ω]
估计 data 的功率谱密度.
PowerSpectralDensity[data,ω,sspec]
估计平滑规范 sspec 下 data 的功率谱密度.
PowerSpectralDensity[tproc,ω]
表示时间序列过程 tproc 的功率谱密度.
更多信息和选项

- PowerSpectralDensity 也称为能量谱密度.
- 对于弱平稳时间序列过程,PowerSpectralDensity[tproc,ω] 被定义为
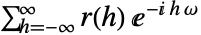 ,其中
,其中 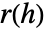 表示 CovarianceFunction[proc,h].
表示 CovarianceFunction[proc,h]. - 可以给出下列平滑规范 sspec:
-
c 使用 c 作为截止点 w 使用窗函数 w {c,w} 同时使用截止点和窗函数 - 对于窗函数 w 和正整数 c,PowerSpectralDensity[data,ω,{c,w}] 用
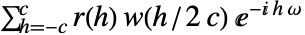 计算,其中
计算,其中 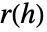 被定义为 CovarianceFunction[data,h].
被定义为 CovarianceFunction[data,h]. - 默认情况下,选择截止点 c 为
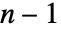 ,其中
,其中 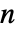 是 data 的长度,而窗函数是 DirichletWindow.
是 data 的长度,而窗函数是 DirichletWindow. - 窗函数
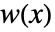 是偶函数,满足
是偶函数,满足 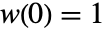 ,
,![TemplateBox[{{w, (, x, )}}, Abs]<=1 TemplateBox[{{w, (, x, )}}, Abs]<=1](Files/PowerSpectralDensity.zh/9.png) ,当
,当 ![TemplateBox[{x}, Abs]>1/2 TemplateBox[{x}, Abs]>1/2](Files/PowerSpectralDensity.zh/10.png) 时
时 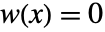 ,包括诸如 HammingWindow、ParzenWindow 等标准窗函数.
,包括诸如 HammingWindow、ParzenWindow 等标准窗函数. - 窗函数可由数值列表 {w0,…} 给出,其中
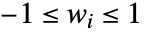 ,对于向量值序列,会将窗函数对称运用.
,对于向量值序列,会将窗函数对称运用. - PowerSpectralDensity 使用 FourierParameters 选项. FourierParameters 的常见设置包括:
-
{1,1} 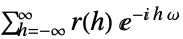
缺省设置 {-1,1} 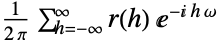
常用于时间序列 {a,b} 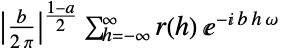
通用设置
范例
打开所有单元关闭所有单元范围 (14)
平滑 (5)
使用 NuttallWindow 计算功率谱密度:
和用 TukeyWindow 作为窗函数的结果进行比较:
随机过程 (5)
ARProcess 的功率谱密度:
向量 ARProcess:
MAProcess 的功率谱密度:
向量 MAProcess:
ARMAProcess 的功率谱密度:
向量 ARMAProcess:
向量 FARIMAProcess:
向量 SARMAProcess:
选项 (2)
属性和关系 (11)
时间序列的功率谱密度是 CovarianceFunction 的变换:
数据的功率谱密度是样本 CovarianceFunction 的变换:
运用 ListFourierSequenceTransform:
和 SamplePowerSpectralDensity 比较:
和 MAProcess 的特例进行比较:
谐波频率的功率谱密度和 PeriodogramArray 相关:
和 PeriodogramArray 比较:
用 TransferFunctionModel 来计算时间序列的 PowerSpectralDensity:
文本
Wolfram Research (2012),PowerSpectralDensity,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.
CMS
Wolfram 语言. 2012. "PowerSpectralDensity." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSpectralDensity.html.
APA
Wolfram 语言. (2012). PowerSpectralDensity. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PowerSpectralDensity.html 年