Prime[n]
第 n 番目の素数 ![]() を与える.
を与える.


Prime
Prime[n]
第 n 番目の素数 ![]() を与える.
を与える.
詳細
- Primeは素数列としても知られている.
- 記号操作・数値操作の両方に適した数学的整数関数である.
![TemplateBox[{n}, Prime] TemplateBox[{n}, Prime]](Files/Prime.ja/2.png) は,1より大きくそれ自身より小さい整数では割れない
は,1より大きくそれ自身より小さい整数では割れない ![TemplateBox[{{n, -, 1}}, Prime] TemplateBox[{{n, -, 1}}, Prime]](Files/Prime.ja/3.png) より大きい最小の正の整数である.最初の素数
より大きい最小の正の整数である.最初の素数 ![TemplateBox[{1}, Prime] TemplateBox[{1}, Prime]](Files/Prime.ja/4.png) は整数2である.
は整数2である.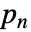 は
は 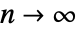 のとき
のとき 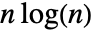 と漸近的に等しい.
と漸近的に等しい.
例題
すべて開く すべて閉じるスコープ (10)
アプリケーション (38)
基本的なアプリケーション (9)
近似 (3)
整数論 (14)
ジャンピングチャンピオン(連続する素数間で最も頻出する差)を求める:
ゴールドバッハ(Goldbach)の予想,つまり![]() となるような素数対(
となるような素数対(![]() ,
, ![]() )を求める:
)を求める:
素数階乗(階乗と同じような連続する素数の乗算)を n 番目の素数まで計算する:
チェビシェフ(Chebyshev)のシータ関数をプロットする:
連続する素数 pnと pn+1のすべてのペアについて √pn+1-√pn<1であるとするアンドリカ(Andrica)の予想をプロットする:
pnと pn+1が2より大きい連続する素数なら,(pn)2と(pn+1)2の間に少なくとも4つの素数が存在するというブロカール(Brocard)の予想をプロットする:
特殊数列 (12)
![]() もまた素数なら,素数
もまた素数なら,素数 ![]() はソフィー・ジェルマン(Sophie Germain)素数である:
はソフィー・ジェルマン(Sophie Germain)素数である:
フェルマ(Fermat)素数(![]() が素数であるようなフェルマ数
が素数であるようなフェルマ数 ![]() )は5つある:
)は5つある:
![]() より小さいヴィーフェリッヒ(Wieferich)素数(
より小さいヴィーフェリッヒ(Wieferich)素数(![]() で
で![]() が割れる素数
が割れる素数 ![]() )は2つある:
)は2つある:
ピタゴラス素数は2つの数列の合計,つまり素数 ![]() として書くことができる:
として書くことができる:
ラマヌジャン(Ramanujan)素数は,すべてのx≥ Rnについて π(x) - π(x/2) ≥ n である最小の数 Rnである:
n 番目のラマヌジャン素数とPrimeの差:
ガウス素数の配列プロット.ガウス整数 ![]() (
( ![]() と
と ![]() が非零のとき
が非零のとき ![]() は素数.あるいは,
は素数.あるいは,![]() のとき
のとき ![]() .あるいは
.あるいは ![]() のとき
のとき ![]() ):
):
特性と関係 (8)
関連項目
NextPrime RandomPrime PrimeQ PrimePowerQ CompositeQ PrimePi Primes PrimeZetaP Zeta MersennePrimeExponent FactorInteger PerfectNumber EulerPhi
Function Repository: LargestPrimeGap TwinPrimes TwinPrime
テクニカルノート
履歴
1988 で導入 (1.0) | 2020 で更新 (12.1)
テキスト
Wolfram Research (1988), Prime, Wolfram言語関数, https://reference.wolfram.com/language/ref/Prime.html (2020年に更新).
CMS
Wolfram Language. 1988. "Prime." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Prime.html.
APA
Wolfram Language. (1988). Prime. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Prime.html
BibTeX
@misc{reference.wolfram_2025_prime, author="Wolfram Research", title="{Prime}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Prime.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_prime, organization={Wolfram Research}, title={Prime}, year={2020}, url={https://reference.wolfram.com/language/ref/Prime.html}, note=[Accessed: 18-February-2026]}