Prime[n]
给出第 n![]() 个质数
个质数 ![]() .
.


Prime
Prime[n]
给出第 n![]() 个质数
个质数 ![]() .
.
更多信息
- Prime 也称为质数序列.
- 整数数学函数,适用于符号和数字操作.
![TemplateBox[{n}, Prime] TemplateBox[{n}, Prime]](Files/Prime.zh/3.png) 是大于
是大于 ![TemplateBox[{{n, -, 1}}, Prime] TemplateBox[{{n, -, 1}}, Prime]](Files/Prime.zh/4.png) 的最小正整数,该整数不能被任何大于1且小于其自身的任何整数整除. 第一个质数
的最小正整数,该整数不能被任何大于1且小于其自身的任何整数整除. 第一个质数 ![TemplateBox[{1}, Prime] TemplateBox[{1}, Prime]](Files/Prime.zh/5.png) 是整数 2.
是整数 2.- 当
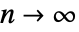 时,
时,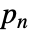 渐近地等价于
渐近地等价于 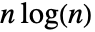 .
.
范例
打开所有单元 关闭所有单元范围 (10)
应用 (38)
基本应用 (9)
数论 (14)
特殊序列 (12)
如果 ![]() 也是素数,则素数
也是素数,则素数 ![]() 是 Sophie Germain 素数:
是 Sophie Germain 素数:
拉马努金素数是对于全部 x≥ Rn,使得 π(x) - π(x/2) ≥ n 成立的最小数 Rn:
第 n 个拉马努金素数与 Prime 之差:
对于高斯整数 ![]() ,如果满足
,如果满足 ![]() 和
和 ![]() 非零,
非零,![]() 为素数,或
为素数,或 ![]() ,
,![]() ,或
,或 ![]() 则
则 ![]() ,则为高斯素数. 以下是高斯素数的阵列图:
,则为高斯素数. 以下是高斯素数的阵列图:
属性和关系 (8)
技术笔记
历史
1988年引入 (1.0) | 在以下年份被更新:2020 (12.1)
文本
Wolfram Research (1988),Prime,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Prime.html (更新于 2020 年).
CMS
Wolfram 语言. 1988. "Prime." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/Prime.html.
APA
Wolfram 语言. (1988). Prime. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Prime.html 年
BibTeX
@misc{reference.wolfram_2025_prime, author="Wolfram Research", title="{Prime}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Prime.html}", note=[Accessed: 15-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_prime, organization={Wolfram Research}, title={Prime}, year={2020}, url={https://reference.wolfram.com/language/ref/Prime.html}, note=[Accessed: 15-February-2026]}