求一个矩阵的伪逆矩阵.


PseudoInverse
求一个矩阵的伪逆矩阵.
更多信息和选项

- PseudoInverse 适用于符号矩阵和数值矩阵.
- 对于方阵,PseudoInverse 给出 Moore–Penrose 逆矩阵.
- 对于数值矩阵,PseudoInverse 是基于 SingularValueDecomposition.
- PseudoInverse[m,Tolerance->t] 指定去掉小于最大奇异值的 t 倍的奇异值.
- 缺省设置 Tolerance->Automatic,去掉小于 10-p 的 100 倍的奇异值,其中 p 是 Precision[m].
- 对于非奇异方阵 M,伪逆
![TemplateBox[{M}, PseudoInverse] TemplateBox[{M}, PseudoInverse]](Files/PseudoInverse.zh/1.png) 等价于标准逆矩阵
等价于标准逆矩阵 ![TemplateBox[{M}, Inverse] TemplateBox[{M}, Inverse]](Files/PseudoInverse.zh/2.png) .
. - PseudoInverse[m] 的 StandardForm 和 TraditionalForm 为
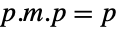 . »
. »
范例
打开所有单元 关闭所有单元基本范例 (5)
范围 (11)
特殊矩阵 (4)
选项 (1)
应用 (8)
求解方程 (4)
最小二乘和曲线拟合 (4)
使用 LeastSquares[m,b] 也可以得到这个结果:
使用 Minimize 确认答案:
使用 LeastSquares[m,b] 也可以得到这个结果:
使用 Minimize 确认该答案:
PseudoInverse 可用于找到数据的最佳拟合曲线. 考虑如下数据:
使用 Fit 验证系数:
使用 Fit 验证系数:
属性和关系 (14)
PseudoInverse 是对合的,即 ![]() :
:
PseudoInverse 与 Transpose 对易,即 ![]() :
:
也与 Conjugate 对易,即 ![]() :
:
因此其与 ConjugateTranspose 对易,即 ![]() :
:
PseudoInverse 满足 Moore–Penrose 方程 [更多信息]:
若 MatrixRank[m] 等于 ![]() 的列数,则
的列数,则 ![]() :
:
特别是,PseudoInverse[m] 是 m 的左逆:
如果 MatrixRank[m] 等于 ![]() 的行数,则
的行数,则 ![]() :
:
特别是,PseudoInverse[m] 是 m 的右逆:
对于对角矩阵 d,PseudoInverse[d] 是非零元素倒置的转置:
若 a 为一个 ![]() 矩阵且 MatrixRank[a]==m,QRDecomposition 会给出伪逆矩阵:
矩阵且 MatrixRank[a]==m,QRDecomposition 会给出伪逆矩阵:
PseudoInverse[m] 可以 ![]() 形式进行计算,其中
形式进行计算,其中 ![]() 表示 DrazinInverse:
表示 DrazinInverse:
LeastSquares 和 PseudoInverse 都可用于求解最小二乘问题:
将 ![]() 的 NullSpace 中的任何向量添加到
的 NullSpace 中的任何向量添加到 ![]() 不会改变残差:
不会改变残差:
参见
Inverse LeastSquares Fit SingularValueDecomposition SingularValueList DrazinInverse
Function Repository: ProjectionMatrix
技术笔记
-
▪
- 高级矩阵运算
相关指南
-
▪
- 基于矩阵的最小化 ▪
- 矩阵运算 ▪
- 矩阵和线性代数 ▪
- 线性系统 ▪
- GPU 计算 ▪
- 符号向量、矩阵和数组 ▪
- NVIDIA GPU 计算
历史
1988年引入 (1.0) | 在以下年份被更新:2003 (5.0) ▪ 2025 (14.3)
文本
Wolfram Research (1988),PseudoInverse,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PseudoInverse.html (更新于 2025 年).
CMS
Wolfram 语言. 1988. "PseudoInverse." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/PseudoInverse.html.
APA
Wolfram 语言. (1988). PseudoInverse. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PseudoInverse.html 年
BibTeX
@misc{reference.wolfram_2025_pseudoinverse, author="Wolfram Research", title="{PseudoInverse}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/PseudoInverse.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_pseudoinverse, organization={Wolfram Research}, title={PseudoInverse}, year={2025}, url={https://reference.wolfram.com/language/ref/PseudoInverse.html}, note=[Accessed: 03-March-2026]}