RFixedPoints

RFixedPoints[eqn,a[n],n]

再帰方程式の固定点を与える．

RFixedPoints[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

再帰方程式系の固定点を与える．

詳細とオプション

  • 固定点は，平衡点あるいは停留点としても知られている．
  • RFixedPointsは，通常，生態学，経済学，技術におけるモデリングで頻繁に発生する，非線形離散系のすべての固定点を見付けるために使われる．これらの固定点における局所動作はRStabilityConditionsを使って解析できる．
  • 再帰方程式 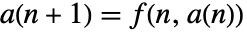の系について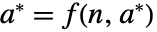．のときかつそのときに限って点 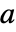は固定点である．実際，初期値 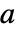は静止したままである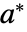．で初期化すると 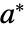に静止したままになる．
  • RFixedPointsは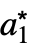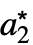，{{,,…},…}の形のリストを返す．ただし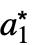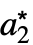，{,,…}は固定点である．
  • RFixedPointsは線形と非線形の常微分方程式に使うことができる．
  • 次は，使用可能なオプションである．
  • Assumptions$Assumptionsパラメータについての仮定

例題

すべて開くすべて閉じる

例  (6)

再帰式 の固定点を求める：

再帰式 の固定点を求める：

再帰式 の固定点を求める：

点の安定性をチェックする：

a のさまざまな値についてのいくつかの解をプロットする：

二次元の系の固定点を求める：

安定性の条件を決定する：

系が安定するパラメータ領域をプロットする：

非線形再帰方程式の固定点を求める：

安定性を判定する：

クモの巣プロットを使って安定性を示す：

系 , について考える：

差分 と を計算して系のベクトル場プロットを生成する：

スコープ  (14)

線形方程式  (4)

再帰式 の固定点を求める：

一次線形非同次方程式：

安定性の条件を決定する：

についての解をプロットする：

についての解をプロットする：

二次線形方程式：

安定性の条件を決定する：

安定領域をプロットする：

三次線形方程式：

安定性の条件を決定する：

安定領域をプロットする：

非線形方程式  (3)

ロジスティック方程式の固定点：

点の安定性を解析する：

解をプロットする：

クモの巣プロットを使って安定性を示す：

Riccati方程式の固定点：

クモの巣プロットを使って安定性を示す：

高次方程式：

線形系  (5)

非結合方程式の線形系の固定点：

定数係数を持つ線形系：

VectorPlotを使って固定点を可視化する：

境界条件がある系を解く：

解をプロットする：

周期係数がある一次の系：

一般解と比較する：

最終的に周期的になる係数がある一次の系：

ランダムな定数係数を持つ10x10離散線形系：

非線形系  (2)

非線形の一次の系：

固定点の安定性を判定する：

線形分数系の固定点と安定性：

VectorPlotを使って点における安定性を可視化する：

アプリケーション  (8)

数値解析  (3)

関数x2-aについてのニュートン・ラフソン(Newton–Raphson)差分方程式を解析する：

固定点を求める：

のときの固定点の安定性を可視化する：

関数x1/3についてのニュートン・ラフソン差分方程式の安定性を解析する：

この方程式は，原点に一つの不安定な固定点を持つ：

点の不安定性は，この場合はニュートン法が使えないことを意味する：

以下のような線形方程式 の系について考える：

この系についてのガウス・サイデル(Gauss–Seidel)差分方程式を構築する：

ガウス・サイデル方程式の固定点を求める：

LinearSolveを使って系を解く：

物理学  (1)

一定温度 の環境内にある温度 の物体について考える．が時間 による物体内の温度変化であるとする．ニュートンの冷却法則によると，物体の温度の変化率は物体とその周囲の温度の差に比例する：

固定点を求める：

なら固定点は安定している：

方程式の解：

冷却過程のシミュレーションを行う：

加熱過程のシミュレーションを行う：

生態学と生物学  (2)

競合種モデルについての安定性解析：

指定された初期条件で方程式を解き，解をプロットする：

捕食者被食者モデルの安定性解析：

モデルのベクトル場プロット：

RecurrenceTableを使ってこの系を数値的に解く：

経済学  (2)

初回入金額 ，年率 ，毎月の引き出し金額 の銀行口座について考える． ヶ月後の貯蓄預金口座の金額は次の再帰方程式を満足する：

この方程式には不安定な固定点 がある：

なら預金口座の残高は毎月増加する：

ロジスティック方程式の安定性解析：

固定点の安定性をチェックする：

パラメータ の指定された範囲における安定性をチェックする：

についての安定性を可視化する：

についての安定性を可視化する：

特性と関係  (8)

RFixedPointsは再帰方程式の固定点を返す：

RStabilityConditionsを使って，再帰方程式のすべての固定点の安定性を判定する：

特定の固定点における安定性を解析する：

RFixedPointsを使って非線形再帰方程式のすべての固定点を求める：

Solveを使って固定点を求める：

n 次再帰方程式の固定点は n 次元ベクトルである：

n 個の一次再帰方程式の系の固定点は n 次元ベクトルである：

2つの常微分方程式の系の固定点を求める：

RSolveValueで，固定点を初期条件として使って系を解く：

RSolveValueを使って指定された初期条件で系を解く：

解をプロットする：

非線形常微分方程式の安定性を解析する：

RecurrenceTableを使って常微分方程式を解く：

解をプロットする：

最終的に定数になる係数を持つ再帰方程式の安定性を解析する：

AsymptoticRSolveValueを使って級数解を求める：

漸近解をプロットする：

Wolfram Research (2024), RFixedPoints, Wolfram言語関数， https://reference.wolfram.com/language/ref/RFixedPoints.html.

テキスト

Wolfram Research (2024), RFixedPoints, Wolfram言語関数， https://reference.wolfram.com/language/ref/RFixedPoints.html.

CMS

Wolfram Language. 2024. "RFixedPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RFixedPoints.html.

APA

Wolfram Language. (2024). RFixedPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RFixedPoints.html

BibTeX

@misc{reference.wolfram_2024_rfixedpoints, author="Wolfram Research", title="{RFixedPoints}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RFixedPoints.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rfixedpoints, organization={Wolfram Research}, title={RFixedPoints}, year={2024}, url={https://reference.wolfram.com/language/ref/RFixedPoints.html}, note=[Accessed: 21-November-2024 ]}