RStabilityConditions

RStabilityConditions[eqn,a[n],n]

给出递归方程的不动点和稳定性条件.

RStabilityConditions[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

给出递归方程组的不动点和稳定性条件.

RStabilityConditions[{eqn1,eqn2,…},{a1[n],a2[n],…},n,{pnt1,pnt2,…}]

给出已知不动点的稳定性条件.

更多信息和选项

  • 稳定性又称为渐近稳定性，不动点又称为平衡点或驻点.
  • RStabilityConditions 通常用于定性分析不动点附近的长期行为。如果系统稳定，则只要足够接近固定点，解就会收敛到不动点.
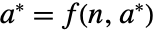  • 对于递归方程组 ，当且仅当 时，点 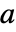为不动点. 实际上，初始值 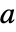保持不变；如果在 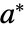处初始化，则保持在 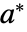处.
  • 当且仅当 且 ，对于足够小的 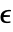，TemplateBox[{{a, (, n, )}, n, infty}, Limit2Arg]=a^* 成立，不动点 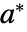是渐近稳定的.
  • RStabilityConditions 返回形如 {{{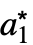,,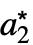…},cond},…} 的列表，其中 {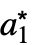,,…} 是不动点.
  • RStabilityConditions 给出了不动点局部稳定的充分条件. 对于线性系统，这些条件也是全局稳定的条件.
  • RStabilityConditions 适用于线性和非线性常微分方程.
  • 可以提供以下选项：
  • Assumptions $Assumptions关于参数的假设

范例

打开所有单元关闭所有单元

基本范例  (8)

求递归 的不动点，并确定其稳定性：

求递归 的不动点，并确定其稳定性：

求递归 的不动点和稳定性条件：

绘制对于不同 a 值的几个解：

二维系统的稳定性分析：

绘制系统稳定的参数区域：

非线性递归方程的稳定性分析：

使用蛛网图来展示稳定性：

考虑方程组 , ：

计算 与 之差，以生成系统的矢量场图：

具有常数系数的线性系统的稳定性：

使用 VectorPlot 来可视化稳定性：

求由三个常微分方程组成的非线性系统的不动点：

研究第一个点的稳定性：

研究第二个点的稳定性：

范围  (14)

线性方程  (4)

对于递归 ，求不动点并确定其稳定性：

一阶线性非齐次方程：

绘制 时解的图形：

绘制 时解的图形：

二阶线性方程：

绘制稳定性区域：

三阶线性方程：

绘制稳定性区域：

非线性方程  (3)

逻辑方程的稳定性：

绘制解的图形：

使用蛛网图来展示稳定性：

Riccati 方程的稳定性：

使用蛛网图来展示稳定性：

高阶方程：

线性系统  (5)

线性非耦合方程组的稳定性：

具有常数系数的线性系统的稳定性：

使用 VectorPlot 来可视化稳定性：

求解具有边界条件的系统：

绘制解的图形：

具有周期系数的一阶系统：

与通解比较：

具有最终周期系数的一阶系统：

分析具有随机常数系数的 10x10 离散线性系统的稳定性：

非线性系统  (2)

非线性一阶系统：

仅检查第一个不动点的稳定性：

仅检查第二个不动点的稳定性：

线性分数系统的稳定性：

使用 VectorPlot 可视化点 处的稳定性：

选项  (1)

Assumptions  (1)

如果没有 Assumptions，稳定性参数的条件为：

使用 Assumptions 通常可以得到简化的条件：

应用  (8)

数值分析  (3)

分析函数 x2-a 的牛顿-拉弗森（Newton–Raphson）差分方程的稳定性：

该方法的递归方程为：

研究系统的稳定性：

可视化 时不动点的稳定性：

分析函数 x1/3 的牛顿-拉弗森差分方程的稳定性：

该方法的递归方程为：

该方程在原点有一个不稳定的不动点：

该点的不稳定性意味着在这种情况下不能使用牛顿法：

考虑一个线性方程组 ，其中：

构建该系统的高斯-赛德尔（Gauss-Seidel）差分方程：

分析高斯-赛德尔方程的稳定性：

使用 LinearSolve 求解方程组：

物理学  (1)

考虑一个处于恒温 的环境中初始温度为 的物体. 令 为物体在时间区间 内的温度变化. 牛顿冷却定律指出，物体温度的变化率与物体温度和其周围环境温度之差成正比：

如果 ，则方程是稳定的：

方程的解：

模拟冷却过程：

模拟加热过程：

生态学和生物学  (2)

竞争物种模型的稳定性分析：

针对给定的初始条件求解方程并绘制解：

捕食者-猎物模型的稳定性分析：

模型的矢量场图：

求解方程组并绘制解的图形：

经济学  (2)

考虑一个银行账户，初始存款为 ，年利率为 ，每月提取金额为 . 储蓄账户在 个月后中的金额满足一个递推方程：

方程有不稳定不动点 ：

如果 ，账户金额将每月增加：

逻辑方程的稳定性分析：

检查不动点的稳定性：

检查参数 在给定范围的稳定性：

可视化 的稳定性：

可视化 的稳定性：

属性和关系  (8)

RStabilityConditions 返回递归方程的不动点和稳定性条件：

使用 RFixedPoints 求递归方程的所有不动点：

分析特定不动点处的稳定性：

使用 RFixedPoints 求非线性递归方程的所有不动点：

使用 Solve 求不动点：

在第一个不动点附近线性化方程：

检查第一个不动点附近的稳定性：

在第二个不动点附近线性化方程：

检查第二个不动点附近的稳定性：

使用 RStabilityConditions 确定非线性方程的稳定性：

n 阶递归方程的不动点是 n 维向量：

由 n 个一阶递归方程组成的系统的不动点是 n 维向量：

分析由两个常微分方程组成的系统的稳定性：

使用 RSolveValue 求解以不动点为初始条件的系统：

使用 RSolveValue 求解给定初始条件下的系统：

绘制解的图形：

分析非线性常微分方程的稳定性：

使用 RecurrenceTable 求解常微分方程：

绘制解的图形：

分析具有最终常数系数的递归方程的稳定性：

使用 AsymptoticRSolveValue 求级数解：

绘制渐近解：

可能存在的问题  (2)

有时稳定性的条件并不是最简单的：

通过进一步处理可以实现进一步简化：

RStabilityConditions 失败，因为给定的点不是不动点：

首先使用 DFixedPoints 找到方程的所有不动点：

Wolfram Research (2024)，RStabilityConditions，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RStabilityConditions.html.

文本

Wolfram Research (2024)，RStabilityConditions，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RStabilityConditions.html.

CMS

Wolfram 语言. 2024. "RStabilityConditions." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RStabilityConditions.html.

APA

Wolfram 语言. (2024). RStabilityConditions. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RStabilityConditions.html 年

BibTeX

@misc{reference.wolfram_2024_rstabilityconditions, author="Wolfram Research", title="{RStabilityConditions}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RStabilityConditions.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rstabilityconditions, organization={Wolfram Research}, title={RStabilityConditions}, year={2024}, url={https://reference.wolfram.com/language/ref/RStabilityConditions.html}, note=[Accessed: 21-November-2024 ]}