RegionDimension
RegionDimension[reg]
領域 reg の幾何次元を与える.
詳細とオプション

- reg の幾何次元 d は,d 次元の球体がその領域に完全に埋め込まれるような最大の d である.
- 異なる次元の領域の一般的な名称
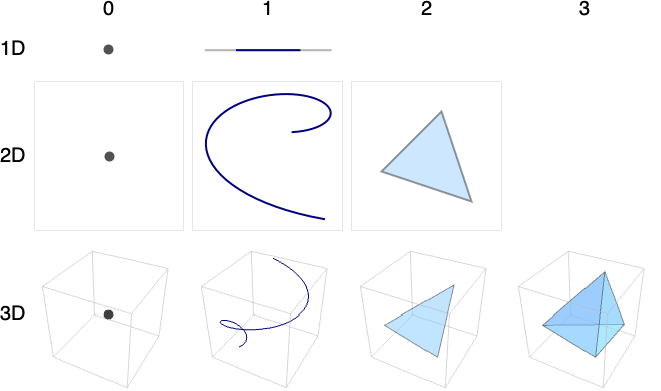
-
0 点 1 線,曲線,弧,線分,区間 2 平面,曲面 3 立体,体積 - 以下の例では,行が埋込み次元に,列がRegionDimensionに対応する.
- RegionDimensionは,パラメータについての仮定の指定に使うことができるAssumptionsオプションを取る.
例題
すべて開くすべて閉じるスコープ (17)
特別な領域 (4)
数式定義領域 (3)
ImplicitRegionとして表された円板の次元:
ParametricRegionとして表された円板の次元:
ImplicitRegionは,次元が異なる複数の成分を持つことができる:
RegionDimensionは最大次元を与える:
メッシュ領域 (4)
派生領域 (4)
地理的領域 (2)
アプリケーション (8)
RegionDimensionを使って立体と曲面の違いを示す:
RegionMeasureの単位は ![]() である.ただし,
である.ただし,![]() は単位長で
は単位長で ![]() である:
である:
RegionMeasureからの結果と比較する:
MeshPrimitivesを使い,MeshRegionプリミティブを次元ごとに抽出する:
全次元のプリミティブのみを選択(Select)する:
特性と関係 (8)
RegionDimensionは,次元が異なるさまざまな部分の最大次元を与える:
RegionDimensionは最大次元である:
RegionEmbeddingDimensionは,領域が存在する空間の次元である:
これは,常にRegionDimension以上である:
DimensionalMeshComponentsは,メッシュを次元が異なる部分ごとに分割する:
RegionMeasureおよびRegionCentroidは次元依存である:
RegionBoundaryのRegionDimensionは入力の領域次元よりも1小さい:
RegionUnionのRegionDimensionは入力の最大次元に等しい:
RegionIntersectionのRegionDimensionは,最小の入力次元より大きくはない:
テキスト
Wolfram Research (2014), RegionDimension, Wolfram言語関数, https://reference.wolfram.com/language/ref/RegionDimension.html.
CMS
Wolfram Language. 2014. "RegionDimension." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDimension.html.
APA
Wolfram Language. (2014). RegionDimension. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDimension.html