WOLFRAM

Wolfram 语言与系统参考资料中心

RollPitchYawMatrix[{α,β,γ}]

给出三维旋转矩阵，通过绕初始 轴旋转 α，再绕初始 轴旋转 β，然后绕初始 轴旋转 γ 形成.

RollPitchYawMatrix[{α,β,γ},{a,b,c}]

给出三维旋转矩阵，通过绕固定 a 轴旋转 α，再绕固定 b 轴旋转 β，然后绕固定 c 轴旋转 γ 形成.

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
选项  
TargetStructure  
应用  
插图  
陀螺仪  
属性和关系  
可能存在的问题  
巧妙范例  
参见
相关指南
历史
按以下格式引用：

RollPitchYawMatrix

RollPitchYawMatrix[{α,β,γ}]

给出三维旋转矩阵，通过绕初始 轴旋转 α，再绕初始 轴旋转 β，然后绕初始 轴旋转 γ 形成.

RollPitchYawMatrix[{α,β,γ},{a,b,c}]

给出三维旋转矩阵，通过绕固定 a 轴旋转 α，再绕固定 b 轴旋转 β，然后绕固定 c 轴旋转 γ 形成.

更多信息和选项

  • RollPitchYawMatrix 也称为倾斜-仰角-航向矩阵或卡丹矩阵. 角度 {α,β,γ} 通常指的是 Cardan 角、Tait–Bryan 角、航海角、倾斜-仰角-航向或横滚-俯仰-偏航.
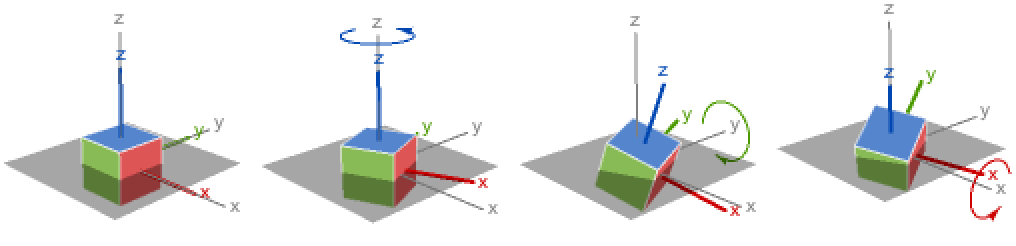
  • RollPitchYawMatrix 通常用于指定绕坐标轴进行基本旋转的结果，其中每个旋转指的是初始的或外在的坐标标架.
  • RollPitchYawMatrix[{α,β,γ}] 等价于 RollPitchYaw[{α,β,γ},{3,2,1}].
  • RollPitchYawMatrix[{α,β,γ},{a,b,c}] 等价于 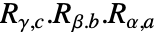，其中 Rα,a=RotationMatrix[α,UnitVector[3,a]]，依此类推.
  • 默认 z-y-x 旋转 RollPitchYawMatrix[{α,β,γ},{3,2,1}]：
  • 旋转轴 a、b 和 c 可以是任意整数 1、2 或 3，但只有12种组合足够通用到可用于指定任意三维旋转.
  • 第一个和最后一个轴重复的旋转：
  • {3,2,3}z-y-z 旋转
    {3,1,3}z-x-z 旋转
    {2,3,2}y-z-y 旋转
    {2,1,2}y-x-y 旋转
    {1,3,1}x-z-x 旋转
    {1,2,1}x-y-x 旋转
  • 三个轴都不同的旋转：
  • {1,2,3}x-y-z r旋
    {1,3,2}x-z-y 旋转
    {2,1,3}y-x-z 旋转
    {2,3,1}y-z-x 旋转
    {3,1,2}z-x-y 旋转
    {3,2,1}z-y-x 旋转 (默认)
  • 随后的轴重复的旋转仍将生成旋转矩阵，但不能使用 RollPitchYawAngles 进行唯一反转.
  • RollPitchYawMatrix 支持选项 TargetStructure，该选项指定了返回的矩阵的结构. TargetStructure 的可能的设置包括：
  • Automatic自动选择返回的形式
    "Dense"用稠密矩阵表示结果
    "Orthogonal"用正交矩阵表示结果
    "Unitary"用酉矩阵表示结果
  • RollPitchYawMatrix[…,TargetStructureAutomatic] 等价于 RollPitchYawMatrix[…,TargetStructure"Dense"].

范例

打开所有单元 关闭所有单元

基本范例  (2)

标准滚动-俯仰-水平矩阵：

Wolfram Language code: RollPitchYawMatrix[{α, β, γ}] /. {Cos[x_] :> Subscript[c, x], Sin[x_] :> Subscript[s, x]}//MatrixForm

旋转一个轴对齐的单位立方体：

Wolfram Language code: m = RollPitchYawMatrix[{(π/4), (π/3), (3π/4)}];
Wolfram Language code: Graphics3D[GeometricTransformation[Cuboid[], m]]

范围  (5)

给出标准 z-y-x 滚动-俯仰-水平旋转矩阵，其中 ，，且 ：

Wolfram Language code: (m = RollPitchYawMatrix[{(3π/4), (π/3), (π/3)}])//MatrixForm

旋转向量 ：

Wolfram Language code: v1 = {1, 0, 0}; v2 = m.v1

可视化旋转矩阵（红色）：

Wolfram Language code: Graphics3D[{Arrow[{{0, 0, 0}, v1}], Red, Arrow[{{0, 0, 0}, v2}]}]

通过指定第二个参数，给出 x-y-z 滚动-俯仰-水平旋转矩阵：

Wolfram Language code: m = RollPitchYawMatrix[{(3π/4), (π/3), (π/3.)}, {1, 2, 3}]

旋转并可视化向量 {1,0,0}：

Wolfram Language code: v1 = {1, 0, 0}; v2 = m.v1;
Wolfram Language code: Graphics3D[{Arrow[{{0, 0, 0}, v1}], Red, Arrow[{{0, 0, 0}, v2}]}]

用 GeometricTransformation 旋转三维图形中的图元：

Wolfram Language code: m = RollPitchYawMatrix[{(π/4), (π/3), (3π/4)}];
Wolfram Language code: before = {Blue, Cuboid[], Green, Point[{1, 1, 1}]}; after = {Red, GeometricTransformation[Cuboid[], m], Green, GeometricTransformation[Point[{1, 1, 1}], m]};
Wolfram Language code: Graphics3D[{PointSize[.05], before, after}]

用 TransformedRegion 旋转区域：

Wolfram Language code: s1 = [image];
Wolfram Language code: m = RollPitchYawMatrix[{Pi / 4, -Pi / 2, -Pi / 4}];
Wolfram Language code: s2 = TransformedRegion[s1, AffineTransform@m];
Wolfram Language code: {s1, s2}

用 ImageTransformation 旋转三维图像：

Wolfram Language code: r1 = ExampleData[{"TestImage3D", "Orbits"}];
Wolfram Language code: m = RollPitchYawMatrix[{Pi / 4, -Pi / 4, -Pi / 4}];
Wolfram Language code: r2 = ImageTransformation[r1, InverseFunction@AffineTransform@m, PlotRange -> All];
Wolfram Language code: {r1, r2}

选项  (1)

TargetStructure  (1)

以稠密矩阵的形式返回横滚-俯仰-偏航矩阵：

Wolfram Language code: RollPitchYawMatrix[{(3π/4), (π/3), (π/3)}, TargetStructure -> "Dense"]

以正交矩阵的形式返回横滚-俯仰-偏航矩阵：

Wolfram Language code: RollPitchYawMatrix[{(3π/4), (π/3), (π/3)}, TargetStructure -> "Orthogonal"]

以酉矩阵的形式返回横滚-俯仰-偏航矩阵：

Wolfram Language code: RollPitchYawMatrix[{(3π/4), (π/3), (π/3)}, TargetStructure -> "Unitary"]

应用  (6)

插图  (1)

建立一个函数，演示欧拉旋转，显示出正被绕着旋转的轴：

Wolfram Language code: $scene = First@[image];
Wolfram Language code: RollPitchYawRotationIllustration[{α_, β_, γ_}, {a_, b_, c_}] := Map[Graphics3D[GeometricTransformation[$scene, #], PlotRange -> 1.2, ImageSize -> 110, BoxStyle -> LightGray]&, {RollPitchYawMatrix[{0, 0, 0}, {a, b, c}], RollPitchYawMatrix[{α, 0, 0}, {a, b, c}], RollPitchYawMatrix[{α, β, 0}, {a, b, c}], RollPitchYawMatrix[{α, β, γ}, {a, b, c}]} ]

这是 a-b-c 轴旋转的全部六种方式. 首先是标准的 z-y-x 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {3, 2, 1}]

然后是 x-y-z 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {1, 2, 3}]

x-z-y 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {1, 3, 2}]

y-x-z 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {2, 1, 3}]

y-z-x 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {2, 3, 1}]

z-x-y 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {3, 1, 2}]

同样有6种 a-b-a 轴旋转. 首先是 x-y-x 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {1, 2, 1}]

x-z-x 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {1, 3, 1}]

y-x-y 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {2, 1, 2}]

y-z-y 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {2, 3, 2}]

z-x-z 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {3, 1, 3}]

z-y-z 滚动-俯仰-水平旋转：

Wolfram Language code: RollPitchYawRotationIllustration[{Pi / 2, Pi / 2, Pi / 2}, {3, 2, 3}]

陀螺仪  (5)

陀螺仪是一具有枢纽的装置，使得物体能在任意方向自我定向. 被用于各种导航和成像应用中：

Wolfram Language code: ring3 = {Red, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 3], Line[{{{0, 0, 4}, {0, 0, 3}}, -{{0, 0, 4}, {0, 0, 3}}}]}; ring2 = {Blue, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 2], Line[{{{0, 3, 0}, {0, 2, 0}}, -{{0, 3, 0}, {0, 2, 0}}}]}; ring1 = {Green, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 1], Line[{{{0, 0, 1}, {0, 0, 2}}, -{{0, 0, 1}, {0, 0, 2}}}], Orange, Arrow[{{-1, 0, 0}, {1, 0, 0}}]};

可通过将 RollPitchYawMatrix 与环旋转（从最外面的环到最里面的环）的角度结合使用来模拟陀螺仪内物体的定向. 注意这里使用的是 a-b-a 轴系统：

Wolfram Language code: gimbal[{α_, β_, γ_}] := With[{}, Graphics3D[{GeometricTransformation[ring3, RollPitchYawMatrix[{0, 0, γ}, {3, 2, 3}]], GeometricTransformation[ring2, RollPitchYawMatrix[{0, β, γ}, {3, 2, 3}]], GeometricTransformation[ring1, RollPitchYawMatrix[{α, β, γ}, {3, 2, 3}]]}, ViewPoint -> {1.3, -2.4, 2.}, PlotRange -> 3.5, PlotLabel -> NumberForm[MatrixForm[{{α, β, γ}}], 2]]]
Wolfram Language code: Manipulate[gimbal[{α, β, γ}], {{α, 0}, 0, 2Pi, Pi / 32}, {{β, 0}, 0, 2Pi, Pi / 32}, {{γ, 0}, 0, 2Pi, Pi / 32}, SaveDefinitions -> True]

具有 a-b-c 轴旋转的陀螺仪模拟的是初始状态为所有环的轴线互相垂直的陀螺仪系统：

Wolfram Language code: ring3 = {Red, CapForm -> None, Tube[{{-.1, 0, 0}, {.1, 0, 0}}, 3], Line[{{{0, 0, 4}, {0, 0, 3}}, -{{0, 0, 4}, {0, 0, 3}}}]}; ring2 = {Blue, CapForm -> None, Tube[{{0, 0, -.1}, {0, 0, .1}}, 2], Line[{{{0, 3, 0}, {0, 2, 0}}, -{{0, 3, 0}, {0, 2, 0}}}]}; ring1 = {Green, CapForm -> None, Tube[{{0, -.1, 0}, {0, .1, 0}}, 1], Line[{{{1, 0, 0}, {2, 0, 0}}, -{{1, 0, 0}, {2, 0, 0}}}], Orange, Arrow[{{0, -1, 0}, {0, 1, 0}}]};

这里使用的是 x-y-z 滚动-俯仰-水平旋转：

Wolfram Language code: gimbal[{α_, β_, γ_}] := Graphics3D[{GeometricTransformation[ring3, RollPitchYawMatrix[{0, 0, γ}, {1, 2, 3}]], GeometricTransformation[ring2, RollPitchYawMatrix[{0, β, γ}, {1, 2, 3}]], GeometricTransformation[ring1, RollPitchYawMatrix[{α, β, γ}, {1, 2, 3}]]}, ViewPoint -> {1.3, -2.4, 2.}, PlotRange -> 3.5, PlotLabel -> NumberForm[MatrixForm[{{α, β, γ}}], 2]]
Wolfram Language code: Manipulate[gimbal[{α, β, γ}], {{α, 0}, 0, 2Pi, Pi / 32}, {{β, 0}, 0, 2Pi, Pi / 32}, {{γ, 0}, 0, 2Pi, Pi / 32}, SaveDefinitions -> True]

旋转系统可能会产生陀螺仪锁定，这是由于某个角度值降低了系统自由度导致的. 在正常的非锁定的情况下会产生下式：

Wolfram Language code: (m1 = RollPitchYawMatrix[{α, β, γ}] /. {β -> π / 3})//MatrixForm

向量 {1,1,0} 可被旋转到曲面上的任意一点：

Wolfram Language code: ParametricPlot3D[m1.{1, 1, 0}, {α, 0, 2π}, {γ, 0, 2π}]

在锁定的情况下，只有 的差值能够影响旋转：

Wolfram Language code: (m2 = RollPitchYawMatrix[{α, β, γ}] /. {β -> Pi / 2})//TrigReduce//MatrixForm

现在向量{1,1,0} 只能旋转到曲线上的点：

Wolfram Language code: ParametricPlot3D[m2.{1, 1, 0}, {α, 0, 2π}, {γ, 0, 2π}]

当轴 ， 时将发生陀螺仪锁定的情况. 以下是 x-y-x 旋转的例子：

Wolfram Language code: axes = {1, 2, 1};

m1 未锁定和 m2 锁定的情形：

Wolfram Language code: m1 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi / 2}; m2 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi};
Wolfram Language code: {ParametricPlot3D[m1.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}], ParametricPlot3D[m2.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]}

z-y-z 旋转的 m1 未锁定和 m2 锁定的情形：

Wolfram Language code: axes = {3, 2, 3};
Wolfram Language code: m1 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi / 3}; m2 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi};
Wolfram Language code: {ParametricPlot3D[m1.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}], ParametricPlot3D[m2.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]}

如果所有的轴都不同，即 ，陀螺仪锁定将在 时发生. 这是在进行 x-y-z 旋转时：

Wolfram Language code: axes = {1, 2, 3};

m1 锁定和 m2 未锁定的情形：

Wolfram Language code: m1 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi / 2}; m2 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi};
Wolfram Language code: {ParametricPlot3D[m1.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}], ParametricPlot3D[m2.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]}

y-x-z 旋转的 m1 锁定和 m2 未锁定的情形：

Wolfram Language code: axes = {2, 1, 3};
Wolfram Language code: m1 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi / 2}; m2 = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> Pi / 3};
Wolfram Language code: {ParametricPlot3D[m1.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}], ParametricPlot3D[m2.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]}

属性和关系  (11)

RollPitchYawMatrix 对应于3种旋转：

Wolfram Language code: rα = RotationMatrix[α, {0, 0, 1}]; rβ = RotationMatrix[β, {0, 1, 0}]; rγ = RotationMatrix[γ, {1, 0, 0}];
Wolfram Language code: Simplify[rγ.rβ.rα == RollPitchYawMatrix[{α, β, γ}]]

在旋转轴的一般排序时：

Wolfram Language code: rollpitchyawMatrix[{α_, β_, γ_}, {i_, j_, k_}] := RotationMatrix[γ, UnitVector[3, k]].RotationMatrix[β, UnitVector[3, j]].RotationMatrix[α, UnitVector[3, i]];
Wolfram Language code: Simplify[rollpitchyawMatrix[{α, β, γ}, {1, 2, 3}] == RollPitchYawMatrix[{α, β, γ}, {1, 2, 3}]]

使用 RollPitchYawAngles 返回生成相同旋转矩阵的角度：

Wolfram Language code: m1 = RollPitchYawMatrix[{π / 3, π / 2, π / 4}];
Wolfram Language code: m2 = RollPitchYawMatrix[RollPitchYawAngles[m1, {3, 2, 1}]];
Wolfram Language code: m1 == m2

这些角度不必相同：

Wolfram Language code: a1 = {π / 2, π, π / 3}; m1 = RollPitchYawMatrix[a1];
Wolfram Language code: a2 = RollPitchYawAngles[m1, {3, 2, 1}]

但是，两组角度都能生成相同的旋转矩阵：

Wolfram Language code: RollPitchYawMatrix[a1] == RollPitchYawMatrix[a2]

RollPitchYawMatrix 在各个步骤中相对于全局轴（固定标架）旋转：

Wolfram Language code: Graphics3D[GeometricTransformation[Cuboid[], RollPitchYawMatrix[{π / 2, π / 2, π / 2}, {1, 2, 3}]], PlotRange -> 1]

EulerMatrix 在各个步骤中相对于局部轴（移动标架）旋转：

Wolfram Language code: Graphics3D[GeometricTransformation[Cuboid[], EulerMatrix[{π / 2, π / 2, π / 2}, {1, 2, 3}]], PlotRange -> 1]

如果随后的两个旋转轴相同，即 或 ，则系统具有2个自由度，这里以进行 x-y-y 旋转为例：

Wolfram Language code: axes = {1, 2, 2}; m = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> #}& /@ Range[0, 3Pi / 2, Pi / 2];
Wolfram Language code: ParametricPlot3D[#.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]& /@ m

如果所有旋转轴相同，即 ，则系统仅有1个自由度，这里以进行 x-x-x 旋转为例：

Wolfram Language code: axes = {1, 1, 1}; m = RollPitchYawMatrix[{α, β, γ}, axes] /. {β -> #}& /@ Range[0, 3Pi / 2, Pi / 2];
Wolfram Language code: ParametricPlot3D[#.{1, 1, 1}, {α, 0, 2π}, {γ, 0, 2π}]& /@ m

RollPitchYawMatrix[{α,β,γ},{a,b,c}] 等同于 EulerMatrix[{γ,β,α},{c,b,a}]：

Wolfram Language code: RollPitchYawMatrix[{α, β, γ}, {1, 2, 3}] == EulerMatrix[{γ, β, α}, {3, 2, 1}]

RollPitchYawMatrix 以3种轴向旋转的方式对任意旋转进行参数化：

Wolfram Language code: v = {1, 0, 0};
Wolfram Language code: RollPitchYawMatrix[{Pi / 4, -Pi / 4, 0}].v

对于绕一般轴的旋转，使用 RotationMatrix：

Wolfram Language code: RotationMatrix[Pi / 2, {1, 0, 1}].v

RollPitchYawMatrix 仅应用于 ：

Wolfram Language code: RollPitchYawMatrix[{Pi / 4, 0, 0}].{1, 0, 0}

对于一般的维数，使用 RotationMatrix：

Wolfram Language code: RotationMatrix[Pi / 4].{1, 0}
Wolfram Language code: RotationMatrix[Pi / 4, {{1, 0, 0, 0}, {0, 1, 0, 0}}].{1, 0, 0, 0}

RollPitchYawMatrix 是一个行列式为1的正交矩阵：

Wolfram Language code: m = RollPitchYawMatrix[{α, β, γ}];
Wolfram Language code: OrthogonalMatrixQ[m]
Wolfram Language code: Det[m]//Simplify

RollPitchYawMatrix 的逆是它的转置矩阵：

Wolfram Language code: m = RollPitchYawMatrix[{α, β, γ}];
Wolfram Language code: Simplify[Transpose[m] == Inverse[m]]

RollPitchYawMatrix[{α,β,γ},{a,b,c}] 的逆矩阵是RollPitchYawMatrix[{-γ,-β,-α},{c,b,a}]：

Wolfram Language code: Simplify[Inverse[RollPitchYawMatrix[{α, β, γ}, {1, 2, 3}]] == RollPitchYawMatrix[{-γ, -β, -α}, {3, 2, 1}]]

可能存在的问题  (1)

RollPitchYawMatrix 允许一样的连续轴，这会产生一个旋转矩阵：

Wolfram Language code: m = RollPitchYawMatrix[{Pi, Pi / 2, Pi / 8}, {1, 1, 2}]
Wolfram Language code: {OrthogonalMatrixQ[m], Det[m]}//Simplify

然而，RollPitchYawAngles 要求连续轴是不同的：

Wolfram Language code: RollPitchYawAngles[m, {1, 1, 2}]

这是因为如果连续轴相等，有些旋转矩阵不能表示：

Wolfram Language code: m1 = RollPitchYawMatrix[{Pi / 3, 0, 0}, {3, 2, 1}]
Wolfram Language code: m2 = RollPitchYawMatrix[{α, β, γ}, {1, 1, 2}]
Wolfram Language code: FindInstance[And@@Thread[m1 == m2], {α, β, γ}]

巧妙范例  (2)

使用 GeometricTransformation 通过角度范围可视化球的旋转：

Wolfram Language code: Graphics3D[GeometricTransformation[{Hue[# / 4Pi], Sphere[{5, 0, 0}, 1]}, RollPitchYawMatrix[{#, Pi / 4, # * 4}]]& /@ Range[0, 2Pi, Pi / 64]]

一组随机旋转四面体的集合：

Wolfram Language code: Graphics3D[GeometricTransformation[{Hue[Total@# / 6Pi], Tetrahedron[{{-1, -(3 Sqrt[3]/8), -(3/8)}, {1, -(3 Sqrt[3]/8), -(3/8)}, {0, (5 Sqrt[3]/8), -(3/8)}, {0, (Sqrt[3]/8), (9/8)}}]}, RollPitchYawMatrix[#]]& /@ RandomReal[{0, 2Pi}, {10, 3}]]
Wolfram Research (2015)，RollPitchYawMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html （更新于 2024 年）.

文本

Wolfram Research (2015)，RollPitchYawMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html （更新于 2024 年）.

CMS

Wolfram 语言. 2015. "RollPitchYawMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html.

APA

Wolfram 语言. (2015). RollPitchYawMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html 年

BibTeX

@misc{reference.wolfram_2026_rollpitchyawmatrix, author="Wolfram Research", title="{RollPitchYawMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html}", note=[Accessed: 07-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_rollpitchyawmatrix, organization={Wolfram Research}, title={RollPitchYawMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/RollPitchYawMatrix.html}, note=[Accessed: 07-November-2026]}