RootMeanSquare
✖
RootMeanSquare
Details
- RootMeanSquare measures scale of data or distributions.
- RootMeanSquare[list] gives the square root of the second sample moment.
- For the list {x1,x2,…,xn}, the root mean square is given by
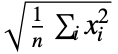 .
. - RootMeanSquare handles both numerical and symbolic data.
- RootMeanSquare[{{x1,y1,…},{x2,y2,…},…}] gives {RootMeanSquare[{x1,x2,…}],RootMeanSquare[{y1,y2,…}]}.
- RootMeanSquare[dist] is equivalent to Sqrt[Expectation[x2,xdist]].
Examples
open allclose allBasic Examples (3)Summary of the most common use cases
RootMeanSquare of a list:
https://wolfram.com/xid/0g7itfcdyf2-xif
RootMeanSquare of columns of a matrix:
https://wolfram.com/xid/0g7itfcdyf2-vu6sr
RootMeanSquare of a parametric distribution:
https://wolfram.com/xid/0g7itfcdyf2-n3bzeg
Scope (14)Survey of the scope of standard use cases
Data (10)
Exact input yields exact output:
https://wolfram.com/xid/0g7itfcdyf2-ug7y2
https://wolfram.com/xid/0g7itfcdyf2-bcry2t
Approximate input yields approximate output:
https://wolfram.com/xid/0g7itfcdyf2-ksx55
https://wolfram.com/xid/0g7itfcdyf2-d02ofx
RootMeanSquare for a matrix gives columnwise means:
https://wolfram.com/xid/0g7itfcdyf2-ezu2uz
https://wolfram.com/xid/0g7itfcdyf2-nknun
https://wolfram.com/xid/0g7itfcdyf2-ma3v2m
SparseArray data can be used just like dense arrays:
https://wolfram.com/xid/0g7itfcdyf2-n691tv
https://wolfram.com/xid/0g7itfcdyf2-drrysl
Compute results for a SparseArray:
https://wolfram.com/xid/0g7itfcdyf2-l4ct3
https://wolfram.com/xid/0g7itfcdyf2-d6csj0

RootMeanSquare for WeightedData:
https://wolfram.com/xid/0g7itfcdyf2-d0wc9z
https://wolfram.com/xid/0g7itfcdyf2-f1vfw
https://wolfram.com/xid/0g7itfcdyf2-qyv0h
RootMeanSquare for EventData:
https://wolfram.com/xid/0g7itfcdyf2-e67u14
https://wolfram.com/xid/0g7itfcdyf2-or2nrz
RootMeanSquare for TimeSeries:

https://wolfram.com/xid/0g7itfcdyf2-hf056t
The root mean square depends only on the values:

https://wolfram.com/xid/0g7itfcdyf2-ikztk4
RootMeanSquare for data involving quantities:
https://wolfram.com/xid/0g7itfcdyf2-jopin9
https://wolfram.com/xid/0g7itfcdyf2-e8c21s
Distributions and Processes (4)
Find the RootMeanSquare for univariate distributions:
https://wolfram.com/xid/0g7itfcdyf2-rxz55
https://wolfram.com/xid/0g7itfcdyf2-hbq28j
https://wolfram.com/xid/0g7itfcdyf2-ek075b
https://wolfram.com/xid/0g7itfcdyf2-lzwoz3
RootMeanSquare for derived distributions:
https://wolfram.com/xid/0g7itfcdyf2-rgc72x
https://wolfram.com/xid/0g7itfcdyf2-byqvvz
https://wolfram.com/xid/0g7itfcdyf2-215ry
https://wolfram.com/xid/0g7itfcdyf2-fq5ptk
RootMeanSquare for distributions with quantities:
https://wolfram.com/xid/0g7itfcdyf2-dqsioj
https://wolfram.com/xid/0g7itfcdyf2-b53jwg
RootMeanSquare for a random process:
https://wolfram.com/xid/0g7itfcdyf2-fugn
https://wolfram.com/xid/0g7itfcdyf2-g9pmgp

Applications (3)Sample problems that can be solved with this function
Root mean square error for a linear fit:
https://wolfram.com/xid/0g7itfcdyf2-lqzjie
https://wolfram.com/xid/0g7itfcdyf2-p1u03
https://wolfram.com/xid/0g7itfcdyf2-cab9e7
https://wolfram.com/xid/0g7itfcdyf2-cwptf9
https://wolfram.com/xid/0g7itfcdyf2-dkujrt
https://wolfram.com/xid/0g7itfcdyf2-yv2c2

Compute the root mean square value of the sample:
https://wolfram.com/xid/0g7itfcdyf2-csnxk
https://wolfram.com/xid/0g7itfcdyf2-ekvqot
https://wolfram.com/xid/0g7itfcdyf2-c3rp5t
Find the root mean square value for the heights of children in a class:
https://wolfram.com/xid/0g7itfcdyf2-cevfij
https://wolfram.com/xid/0g7itfcdyf2-fllmtw

https://wolfram.com/xid/0g7itfcdyf2-celepo
https://wolfram.com/xid/0g7itfcdyf2-cny2bx

Properties & Relations (7)Properties of the function, and connections to other functions
RootMeanSquare is the square root of the Mean of the data squared:
https://wolfram.com/xid/0g7itfcdyf2-793v1
https://wolfram.com/xid/0g7itfcdyf2-b9x4up
https://wolfram.com/xid/0g7itfcdyf2-bhsxlb
RootMeanSquare is equivalent to a scaled Norm:
https://wolfram.com/xid/0g7itfcdyf2-jxw4y8
https://wolfram.com/xid/0g7itfcdyf2-drqfrx
https://wolfram.com/xid/0g7itfcdyf2-cuwc0b
RootMeanSquare of deviations is equivalent to a scaled StandardDeviation:
https://wolfram.com/xid/0g7itfcdyf2-m0xfm
https://wolfram.com/xid/0g7itfcdyf2-hh6mz4
https://wolfram.com/xid/0g7itfcdyf2-i5cfjy
RootMeanSquare of deviations is the square root of a CentralMoment:
https://wolfram.com/xid/0g7itfcdyf2-dso2q7
https://wolfram.com/xid/0g7itfcdyf2-vy95m
https://wolfram.com/xid/0g7itfcdyf2-hfsstq
RootMeanSquare is a scaled EuclideanDistance from the Mean:
https://wolfram.com/xid/0g7itfcdyf2-hx9oab
https://wolfram.com/xid/0g7itfcdyf2-cg5jg0
https://wolfram.com/xid/0g7itfcdyf2-pf9xkh
https://wolfram.com/xid/0g7itfcdyf2-zp24k
RootMeanSquare of a random variable is the square root of an Expectation:
https://wolfram.com/xid/0g7itfcdyf2-c5emif
https://wolfram.com/xid/0g7itfcdyf2-cl5rpb
https://wolfram.com/xid/0g7itfcdyf2-ekl2fe
RootMeanSquare is a measure of scale:
https://wolfram.com/xid/0g7itfcdyf2-bhnrki
https://wolfram.com/xid/0g7itfcdyf2-t94no
https://wolfram.com/xid/0g7itfcdyf2-o9323q

Wolfram Research (2007), RootMeanSquare, Wolfram Language function, https://reference.wolfram.com/language/ref/RootMeanSquare.html (updated 2017).Text
Wolfram Research (2007), RootMeanSquare, Wolfram Language function, https://reference.wolfram.com/language/ref/RootMeanSquare.html (updated 2017).
Wolfram Research (2007), RootMeanSquare, Wolfram Language function, https://reference.wolfram.com/language/ref/RootMeanSquare.html (updated 2017).CMS
Wolfram Language. 2007. "RootMeanSquare." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.
Wolfram Language. 2007. "RootMeanSquare." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.APA
Wolfram Language. (2007). RootMeanSquare. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootMeanSquare.html
Wolfram Language. (2007). RootMeanSquare. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootMeanSquare.htmlBibTeX
@misc{reference.wolfram_2024_rootmeansquare, author="Wolfram Research", title="{RootMeanSquare}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RootMeanSquare.html}", note=[Accessed: 20-December-2024
]}BibLaTeX
@online{reference.wolfram_2024_rootmeansquare, organization={Wolfram Research}, title={RootMeanSquare}, year={2017}, url={https://reference.wolfram.com/language/ref/RootMeanSquare.html}, note=[Accessed: 20-December-2024
]}