RootMeanSquare

RootMeanSquare[list]

list の値の二乗平均平方根を与える．

RootMeanSquare[dist]

分布 dist の二乗平均平方根を与える．

詳細

  • RootMeanSquareは，データまたは分布の測定尺度である．
  • RootMeanSquare[list]は，第2サンプルモーメントの平方根を与える．
  • リスト{x1,x2,…,xn}では，二乗平均平方根は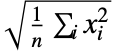で与えられる．
  • RootMeanSquareは，数値データと記号データの両方を扱うことができる．
  • RootMeanSquare[{{x1,y1,…},{x2,y2,…},…}]は{RootMeanSquare[{x1,x2,…}],RootMeanSquare[{y1,y2,…}]}を返す．
  • RootMeanSquare[dist]はSqrt[Expectation[x2,xdist]]に等しい．

例題

すべて開くすべて閉じる

例  (3)

リストのRootMeanSquare：

行列の列のRootMeanSquare：

パラメトリック分布のRootMeanSquare：

スコープ  (14)

データ  (10)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

行列についてのRootMeanSquareは列ごとの平均を与える：

大規模配列に使うことができる：

密な配列と同じようにSparseArrayデータを使うことができる：

SparseArrayの結果を計算する：

WeightedDataについてのRootMeanSquare：

EventDataについてのRootMeanSquare：

TimeSeriesについてのRootMeanSquare：

二乗平均平方根は値のみに依存する：

数量を含むデータについてのRootMeanSquare：

分布と過程  (4)

1変量分布のRootMeanSquareを求める：

多変量分布について：

派生分布のRootMeanSquare：

データ分布：

単位付き数量を含む分布のRootMeanSquare：

ランダム過程のRootMeanSquare：

アプリケーション  (3)

線形フィットの二乗平均平方根誤差：

周期信号からサンプルを取る：

サンプルの二乗平均平方根の値を計算する：

厳密値と比較する：

学級の生徒の身長の二乗平均平方根の値を求める：

特性と関係  (7)

RootMeanSquareは二乗されたデータのMeanの平方根である：

RootMeanSquareはスケールされたNormに等しい：

偏差のRootMeanSquareはスケールされたStandardDeviationに等しい：

偏差のRootMeanSquareはCentralMomentの平方根である：

MeanからのスケールされたEuclideanDistanceとしてのRootMeanSquare：

確率変数のRootMeanSquareはExpectationの平方根である：

RootMeanSquareは測定尺度である：

Wolfram Research (2007), RootMeanSquare, Wolfram言語関数， https://reference.wolfram.com/language/ref/RootMeanSquare.html （2017年に更新）.

テキスト

Wolfram Research (2007), RootMeanSquare, Wolfram言語関数， https://reference.wolfram.com/language/ref/RootMeanSquare.html （2017年に更新）.

CMS

Wolfram Language. 2007. "RootMeanSquare." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.

APA

Wolfram Language. (2007). RootMeanSquare. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootMeanSquare.html

BibTeX

@misc{reference.wolfram_2024_rootmeansquare, author="Wolfram Research", title="{RootMeanSquare}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RootMeanSquare.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rootmeansquare, organization={Wolfram Research}, title={RootMeanSquare}, year={2017}, url={https://reference.wolfram.com/language/ref/RootMeanSquare.html}, note=[Accessed: 18-December-2024 ]}