SameQ

lhs===rhs

式 lhs が rhs と等しい場合にTrueを，その他の場合にはFalseを返す．

詳細

  • SameQは，式の間の厳密な対応を要求する．ただし，例外として両者がReal数については，これらの差が二進法表記で最後の1桁の場合には等しいとみなす．
  • 2===2.は，Falseを与える．
  • e1===e2===e3 は， がすべて互いに等しい場合にTrueを与える．
  • SameQ[]とSameQ[expr]は常にTrueを与える． »

予備知識

  • SameQ[expr1,expr2]は，expr1が expr2と等しいときにはTrueを，それ以外のときにはFalseを返す．ここで言う「等しい」とは，式 expr1と式 expr2のもとになっているFullForm表現が厳密に一致することを意味する．例外として，最終桁のみが異なる実数はSameQであるとみなされる点が挙げられる．SameQ[expr1,expr2]は，expr1===expr2のように3個の等号を使って入力することができる．引数が複数の形SameQ[expr1,expr2,…]（これもexpr1===expr2===…として入力可能）は，すべての式 expriが等しいときかつそのときに限りTrueを返す．
  • 入力形式が異なる式でも，もとになる表現が等しい場合はSameQであることがある．例えば，n! ===Factorial[n]はTrueを返す．一方で，SameQは，数値的には等しいが表現が異なる数の表現を区別する．例えば，SameQ[1,1.]とSameQ[1.,1.+0.I]はどちらもFalseを返す．この動作は，等価性の検証を行い結果が出ない場合は未評価のままに置かれるEqualの動作とは明らかに異なる．
  • SameQは逐語的な一致のみを考慮し，同型は考慮しない．グラフの場合は，IsomorphicGraphQを使って同一性を同型のレベルまで検証すべきである（CanonicalGraphでグラフを標準形に変換し，次にSameQ を使うことも可能である）．
  • SameQは数多くの他のシンボルと関連がある．「1個の等号」シンタックスの expr1=expr2で入力可能なSet[expr1,expr2]は expr2を評価し，その結果が expr1の値になるようにするのに対し，「2個の等号」シンタックス expr1==expr2で入力可能なEqual[expr1,expr2] は，expr1と expr2が数値的に等しい場合にTrueを返す．…=!=…で入力できるUnsameQ はSameQの逆関数である．
  • SameQがFalseを返すケースについて，PossibleZeroQを使って問題の式が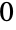になることがあるかどうかを示すことができる．例えば，SameQ[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0]はFalseを返すが，第1引数としてPossibleZeroQを呼ぶとTrueが（0という値が正確に実証されたものではないと言う有益なメッセージとともに）返される．Simplify，FullSimplify，RootReduce等の記号を簡約する関数もまた，（ここに挙げた例を含め）SameQやEqualには不可能な等価性の正確な証明に使われることがある．

例題

すべて開くすべて閉じる

例  (2)

2つの式が等しいかどうかテストする：

==はリテラル値が与えられなければ記号のままになる：

完全形：

スコープ  (4)

文字列の等価性をテストする：

異なる表記法の数字は等しくない：

==は，それにもかかわらず両者を等しいものとして扱う：

近似数は最終ビットが異なっても等しいとみなされる：

複数の式がすべて等しいかどうかテストする：

アプリケーション  (1)

クロネッカー(Kronecker)デルタ（恒等）テンソルを作る：

特性と関係  (4)

SameQは任意数の引数を取ることができる：

SameQ[expri,exprj]がすべての i と j についてTrueであれば，SameQ[expr1,expr2,…]はTrueを与える：

式の一方が他方と同じではないときは，SameQはFalseを与える：

SameQ[expr1,expr2]は!UnsameQ[expr1,expre2]に等しい：

SameQ[…]と!UnsameQ[…]は，引数が2つ以外の場合は等価ではない：

SameQ[]とSameQ[expr]は，常にTrueを与える：

Wolfram Research (1988), SameQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/SameQ.html.

テキスト

Wolfram Research (1988), SameQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/SameQ.html.

CMS

Wolfram Language. 1988. "SameQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SameQ.html.

APA

Wolfram Language. (1988). SameQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SameQ.html

BibTeX

@misc{reference.wolfram_2024_sameq, author="Wolfram Research", title="{SameQ}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/SameQ.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sameq, organization={Wolfram Research}, title={SameQ}, year={1988}, url={https://reference.wolfram.com/language/ref/SameQ.html}, note=[Accessed: 21-November-2024 ]}