Set

lhs=rhs

rhs を評価して，この結果を lhs に割り当てる．これ以降，lhs は現れるたびに rhs で置き換えられる．

{l1,l2,…}={r1,r2,…}

riを評価して，この結果を対応する liに割り当てる．

詳細

  • lhs には，パターンを含む任意の式を使用することができる．
  • f[x_]=x^2が典型的なパターンの割当てである．_が左辺に置かれているが，右辺には置かれていないことに注意．
  • f[args]=rhs の形式の割当ては，シンボル f に結合された変換規則を設定する．
  • 特定のシンボルに結合された異なる規則は，通常，与えられた順に置かれる．新たに与える規則が既存の規則より特殊性が高いと判断された場合には，既存のものに先行して置かれる．規則が使用されるときには，この順にテストされる． »
  • 全く同じ lhs を持つ新しい割当ては，既存のものに上書きされる． »
  • ?f やDefinition[f]を使ってシンボル f に結合されている割当てを見ることができる．
  • 関数にFlatやOrderlessのような属性を割り当てる場合，関数に割当てを実行することに先駆けてこれらの属性を設定しなければならない．
  • Setの属性はHoldFirstである．
  • lhs が f[args]の形式で与えられる場合，args が評価される． »
  • 特殊な関数の中には，s[f[args]]の割当てが，s の代りに自動的に f と結合されるものがある．このような関数としては，Attributes，Default，Format，MessageName，Messages，NそしてOptionsがある． »
  • 評価されないシンボル形式で現れるとき，Setは，必要に応じてネストしている変数が改名されるようスコープ構成として取り扱われる． »
  • lhs=rhs は，何等かの理由で指定された割当てが実行できない場合でも rhs を返す．
  • $RecursionLimitのような大域変数には，一定の範囲，または値のクラスに限って割当てが可能である．

予備知識

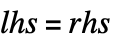  • Setは，式が変数の値になるように評価し割り当てる関数である．式Set[lhs,rhs]は，短縮形のシンタックス lhs=rhs を使って表されることが多い．Setが評価された後で，lhs は，現れるたびに rhs に置換される．lhs の形式によって，結果は関連付けられたOwnValues，DownValues，あるいは特化されたデータ構造のいずれかとして保存される．
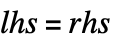  • Setは，rhs に示されるように変換された値に割り当てられる lhs 上のパターンを含むことが多い．例えば，f[x_] = x^2である．lhs=rhs は即座に rhs を評価するので，割当てが行われた後でのみ rhs を評価すべき場合には，SetDelayed（短縮形では:=と書かれる）を代りに使わなければならない．
  • 与えられた記号に関連付けられた割当ては，Definition[f]を使って見ることができる．個々の割当ては，Unsetを使って記号から削除することができる．ClearおよびClearAllはすべての定義を一度に削除する．

例題

すべて開くすべて閉じる

例  (2)

の値を設定する：

の値をクリアする：

複数の値を設定する：

スコープ  (15)

左辺  (7)

通常のプログラムの変数：

「指標付きの変数」の値を設定する：

式から関数を定義する：

Blockを使って一時的に変数を設定する：

リストの一部を設定する：

式の一部を設定する：

行列の行を置換する：

行列の列を置換する：

異なる種類の値  (8)

それ自身の値：

下向きの値：

部分値：

上向きの値：

デフォルトの値とオプション：

数値：

書式の値：

Attributesの定義は，Attributesではなく に関連付けられている：

一般化と拡張  (5)

と に同じ値を設定する：

と に異なる値を設定する：

値を入れ替える：

疎な配列の一部を設定する：

vは，2番目の部分が変えられたが，まだ疎な配列である：

関数の複数の戻り値を個々の変数に割り当てる：

特定の頭部を持ったパターンの定義はその頭部に関連する：

アプリケーション  (6)

2つの数の最大公約数を計算する：

固定点を求める：

ニュートン法を使ってを計算する：

2回以上使われる複雑な式の省略形として変数を使う：

線形方程式系での後退代入のスカラー実装：

線形方程式系における後退代入のベクトル実装：

特性と関係  (9)

即時的定義の右辺は定義が行われたときに評価される：

遅延的定義の右辺は定義が使われるたびに評価される：

定義の左辺の引数は定義が行われる前に評価される：

同じ左辺を持つ定義は前の定義を上書きする：

即時的割当てと遅延的割当てを使って特殊ケースと一般的なケースの定義をする：

より特殊な定義は一般的なものの前に置かれる：

パターン変数は，必要な場合はネストしたスコープの内側で別な名前を付けられる：

Moduleは大域的な記号とは異なる新たな記号を導入する：

Definitionは記号に関連した定義を出力する：

Informationは任意の定義を含んだ記号に関するさまざまな情報を出力する：

OwnValuesは定義された任意の下向きの値に対応する規則のリストを返す：

Unset (=.)を使って特定の左辺を持つ定義を除去する：

すべての定義を除去する：

考えられる問題  (4)

大域変数があると，パターン変数が予期せぬ動作をすることがある：

遅延的割当ては予期した通りに動作する：

暴走定義：

パターン変数は記号ではなく通常割当てはできない：

この目的で局所変数を使う：

上向きの値を使って下付き文字の付いた変数に割り当てる：

下付き文字の付いた変数は指標の付いた変数とは異なる：

おもしろい例題  (1)

2つの数の算術幾何平均を計算する [詳細]：

Wolfram Research (1988), Set, Wolfram言語関数， https://reference.wolfram.com/language/ref/Set.html.

テキスト

Wolfram Research (1988), Set, Wolfram言語関数， https://reference.wolfram.com/language/ref/Set.html.

CMS

Wolfram Language. 1988. "Set." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Set.html.

APA

Wolfram Language. (1988). Set. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Set.html

BibTeX

@misc{reference.wolfram_2024_set, author="Wolfram Research", title="{Set}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Set.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_set, organization={Wolfram Research}, title={Set}, year={1988}, url={https://reference.wolfram.com/language/ref/Set.html}, note=[Accessed: 17-November-2024 ]}