Set

lhs=rhs

计算 rhs 并把结果赋给 lhs. lhs 将总是被 rhs 替换.

{l1,l2,…}={r1,r2,…}

计算 ri，并将结果赋给对应的 li.

更多信息

  • lhs 可以是任何表达式，包括一个模式.
  • f[x_]=x^2 是一个模式的典型赋值. 注意，_ 出现在左边，而不是右边.
  • 形如 f[args]=rhs 的赋值建立与符号 f 相联系的变换法则上.
  • 与一个特定符号相联系的不同规则通常按给出的顺序放置. 如果给出的一个新规则确实比存在的规则更具体，它当然放在它们之前. 这些规则在被使用时将按顺序被检测. »
  • 具有相等 lhs 的新赋值将屏蔽旧的赋值. »
  • 您可以用 ?f 或 Definition[f] 查看与符号 f 相关的所有赋值.
  • 如果要对具有像 Flat 和 Orderless 属性的函数赋值，你必须在赋值之前确保要设置这些属性.
  • Set 具有属性 HoldFirst.
  • 如果 lhs 具有 f[args] 形式，则计算 args. »
  • 对某些函数赋予 s[f[args]] 时，该赋值将自动与 f 相联系，而不是 s. 这些函数包括：Attributes、Default、Format、MessageName、Messages、N 和 Options. »
  • 当它出现在一个未计算的符号形式中时，Set 被视为一个范围结构，以使得嵌套出现的变量在必要时被重命名. »
  • lhs=rhs 返回 rhs，即使因为某些原因该指定的赋值不能执行.
  • 某些类似 $RecursionLimit 的全局变量只能被赋予特定的范围或值的类型.

背景

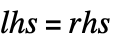  • Set 是一个函数，对表达式求值并将结果作为变量的值. 表达式 Set[lhs,rhs] 通常用简化语法表示成 lhs=rhs 的形式. 在 Set 被求值后，当 lhs 出现时会被替换成 rhs. 根据 lhs 的形式，结果会被存储为与其关联的 OwnValues、DownValues 或特殊的数据结构.
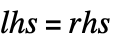  • Set 通常在左侧 lhs 包含模式，用于被赋值为右侧 rhs 指定的转换后的值，例如，f[x_] = x^2. lhs=rhs 会对 rhs 立刻进行求值，这样在需要 rhs 只在应用规则后才被求值的场合，应该用 SetDelayed（简写为 :=）代替.
  • 查看给定符号关联的赋值可以用 Definition[f]. 可以用 Unset 把单独的赋值从符号中移除；Clear 和 ClearAll 可以一次性移除全部的定义.

范例

打开所有单元关闭所有单元

基本范例  (2)

设置 的一个值：

恢复 ：

设置多个值：

范围  (15)

左侧：  (7)

普通的程序变量：

设置“指标变量”的值：

按一个表达式定义一个函数：

用 Block 临时设置变量：

设置列表的子集：

设置表达式的子集：

替换矩阵的一行：

替换矩阵的一列：

不同类型的值：  (8)

本值:

下值（downvalue）：

此值：

上值（upvalue）：

缺省值和选项：

数值值：

格式值：

与 相关的 Attributes 的定义，而不是 Attributes：

推广和延伸  (5)

赋给 和 相同的值：

赋给 和 不同的值：

交换值：

设置稀疏矩阵的子集：

v 依然是一个稀疏矩阵，它的第二个子集改变：

将函数的多个返回值赋给单个变量：

有特定头部的模式的定义与头部相关：

应用  (6)

计算 2 个数的最大公约数：

求出一个固定点：

用牛顿方法计算 ：

使用一个变量作为一个复杂表达式的缩写，并不止调用一次：

在线性方程组中回代的标量执行：

在线性方程组中回代的向量执行：

属性和关系  (9)

当执行定义时，计算立即定义的右边：

每次调用定义时，计算延时定义的右边：

定义左边的参数在定义前计算：

有相同左边的定义，较早的被覆盖：

用立即赋值和延迟赋值执行特殊定义和普通定义：

将特殊定义放在更多普通定义前：

在嵌套范围内尽可能使得模式变量重命名：

Module 引入新的符号，这与全局符号不同：

Definition 输出与符号相关的定义：

Information 输出关于符号的变量信息，包括任何定义：

OwnValues 返回对应定义的任何下值 (downvalue) 的规则列表：

用 Unset (=.) 清除特定左边的定义：

清除所有定义：

可能存在的问题  (4)

存在全局变量时，模式变量可能显示出不能预计的结果：

预计的延迟赋值行为：

超出限制的定义：

非符号的模式变量通常不能被赋值：

因此使用的局部变量：

将上值 (upvalue) 赋给下标变量：

下标变量和指标变量不同：

巧妙范例  (1)

计算两个数的算术-几何均值 [更多信息]：

Wolfram Research (1988)，Set，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Set.html.

文本

Wolfram Research (1988)，Set，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Set.html.

CMS

Wolfram 语言. 1988. "Set." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Set.html.

APA

Wolfram 语言. (1988). Set. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Set.html 年

BibTeX

@misc{reference.wolfram_2024_set, author="Wolfram Research", title="{Set}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Set.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_set, organization={Wolfram Research}, title={Set}, year={1988}, url={https://reference.wolfram.com/language/ref/Set.html}, note=[Accessed: 17-November-2024 ]}