SolidMechanicsStrain

SolidMechanicsStrain[vars,pars,displ]

yields solid mechanics strain with variables vars, parameters pars and displacements displ.

Details

  • SolidMechanicsStrain returns the mechanical strain from a given displacement with dependent variables of displacement 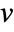, 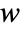and 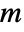in units of 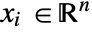, independent variables 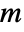in 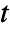and time variable 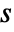in units of .
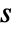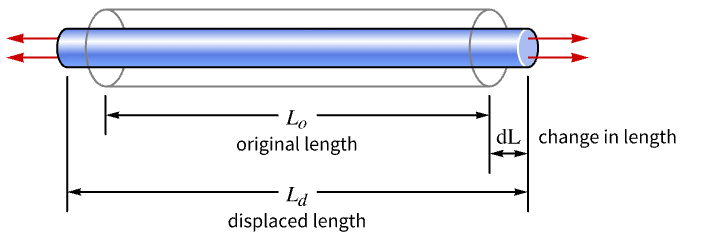
  • Normal strain 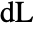where 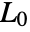is the change in length and 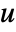the original length.
  • Strains are unitless.
  • SolidMechanicsStrain uses the same variables vars specification as SolidMechanicsPDEComponent.
  • SolidMechanicsStrain uses the same parameter pars specification as SolidMechanicsPDEComponent.
  • Typically the displacement displ is the result of solving a partial differential equation generated with SolidMechanicsPDEComponent.
  • For each dependent variable 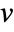, 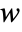and 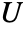given as dependent variable vector 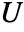in vars, a displacement displ needs to be specified.
  • SolidMechanicsStrain returns a SymmetrizedArray of engineering strains of the form:
  • The 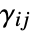represent the normal strain and 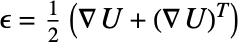represent the shear strains.
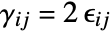  • The default strain measure 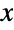is based on an infinitesimal strain tensor model 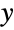and assumes small displacements and small rotations.
  • The shear strains used are engineering shear strains related to the tensorial strain by .
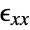  • SolidMechanicsStrain returns strains including 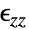initial or thermal strains.
  • SolidMechanicsStress computes stress from SolidMechanicsStrain.

Examples

open allclose all

Basic Examples  (1)

Compute strain from a displacement:

Visualize the strain:

Scope  (4)

Compute the strain from the displacement:

Inspect the engineering strain:

Compute the strain tensor:

Verify the relation between the engineering strain and the strain tensor:

The default usage of engineering strain in the linear elastic regime can be turned off:

Stationary Analysis  (1)

Compute the deflection of a spoon held fixed at the end and with a force applied at the top. Set up variables and parameters:

Set up the PDE and the geometry:

Compute the strain from the displacement:

Visualize the strain:

Stationary Plane Stress Analysis  (1)

Compute the displacement of a rectangular steel plate held fixed at the bottom and with pressures applied at the remaining sides. Set up the region, variables and parameters:

Solve the equations:

Visualize the displacement:

Compute the strain:

Verify that the normal strain in the direction is about 0:

Verify that the normal strain in the direction is about 0:

Find the shear strain:

Stationary Hyperelastic Plane Stress Analysis  (1)

Compute the displacement of a rectangular rubber plate held fixed at the left and with force applied at the right-hand side. Set up the region, variables and parameters:

Solve the equations:

Visualize the displacement:

Compute the strain from the displacement:

Visualize the strain:

Possible Issues  (1)

By default, the solid mechanics framework uses engineering strains for the linear elastic regime. This can be switched off.

Set up a helper function with a solid mechanics PDE model:

Create variables and parameters:

Solve the solid mechanics model with engineering strains:

Solve the solid mechanics model with engineering strains off:

Verify at a specific point that the shear strains of the engineering formulation relate to the normal strain formulation by a factor of 2:

Wolfram Research (2021), SolidMechanicsStrain, Wolfram Language function, https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html (updated 2022).

Text

Wolfram Research (2021), SolidMechanicsStrain, Wolfram Language function, https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html (updated 2022).

CMS

Wolfram Language. 2021. "SolidMechanicsStrain." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html.

APA

Wolfram Language. (2021). SolidMechanicsStrain. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html

BibTeX

@misc{reference.wolfram_2024_solidmechanicsstrain, author="Wolfram Research", title="{SolidMechanicsStrain}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_solidmechanicsstrain, organization={Wolfram Research}, title={SolidMechanicsStrain}, year={2022}, url={https://reference.wolfram.com/language/ref/SolidMechanicsStrain.html}, note=[Accessed: 21-December-2024 ]}