SolidMechanicsStress

SolidMechanicsStress[vars,pars,strain]

yields solid mechanics internal stress with variables vars, parameters pars and total strain strain.

SolidMechanicsStress[vars,pars,strain,displacement]

yields solid mechanics stress for nonlinear material laws.

Details

SolidMechanicsStress returns the mechanical stress from a given total strain with dependent variables of displacement 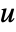, 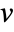and 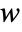in units of 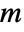, independent variables 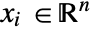in 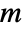and time variable 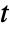in units of .

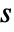Stress is a resistance force per cross-sectional area .
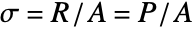Stresses have the unit of .
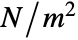SolidMechanicsStress uses the same variables vars specification as SolidMechanicsPDEComponent.
SolidMechanicsStress uses the same parameter pars specification as SolidMechanicsPDEComponent.
A SymmetrizedArray specifies strain.
Typically, strain is the result of SolidMechanicsStrain.
For elastic materials, SolidMechanicsStress uses the elastic strain 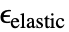to compute the stress:

SolidMechanicsStress subtracts inelastic strains 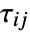such as thermal or initial strains from the given total strain .
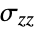SolidMechanicsStress returns a SymmetrizedArray of stresses of the form:

The represent the normal stresses and represent the shear stresses.
SolidMechanicsStress computes the internal stress :

An initial stress 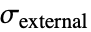can be specified for SolidMechanicsPDEComponent with the "InitialStress" parameter.
For nonlinear materials, SolidMechanicsStress uses the total strain and displacement to compute the stress.

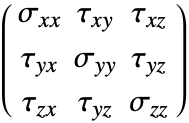
Examples

open allclose all

Basic Examples (1)

Compute stress from a strain:

Visualize the stress:

Scope (4)

Stationary Analysis (1)

Compute the deflection of a spoon held fixed at the end and with a force applied at the top. Set up variables and parameters:

Set up the PDE and the geometry:

Compute the strains from the displacement:

Compute the stresses from the strains:

Visualize the stress:

Stationary Plane Stress Analysis (1)

Compute a plane stress case as an extended model. This allows for the computation of the out-of-plane strain and verifies that the out-of-plane stress is 0. A rectangular steel plate is held fixed at the left and with a forced displacement on the right. Set up the region, variables and parameters. The variables now include all three directions:

Solve the equations with three semi-dependent variables:

Note that now there are three output variables in the list of displacements. Visualize the displacement for the main variables:

Compute the strain:

Note that the strain is a 3×3 array. Visualize the out-of-plane strain:

Compute the stress from the strain:

Note that the stress is a 3×3 array. Verify the plane stress condition:

Stationary Plane Strain Analysis (1)

Compute a plane strain case as an extended model. This allows for the computation of the out-of-plane stress and verifies that the out-of-plane strain is 0. Set up the region, variables and parameters. The variables now include all three directions:

Set up the solid mechanics PDE component:

Set up the PDEs:

Solve the PDE:

Compute the strains from the displacements:

Note that the strain is a 3×3 array. Verify the plane strain condition:

Compute the stress from the strain:

Note that the stress is a 3×3 array. Visualize the out-of-plane stress:

Stationary Hyperelastic Plane Stress Analysis (1)

Compute the displacement of a rectangular rubber plate held fixed at the left and with force applied at the right-hand side. Set up the region, variables and parameters:

Solve the equations:

Visualize the displacement:

Compute the strain from the displacement:

Compute the stress from the strain and displacement:

Visualize the strain:

Possible Issues (1)

In the axisymmetric case, it is important that the displacements specified are functions of the spatial coordinates. To illustrate why, create variables, parameters and displacement functions that are not functions of space:

Note that the generated InterpolatingFunction is not a function of the spatial coordinates and . Now when the strain and stress are computed, it can be seen that in the stress tensor, some interpolating functions also appear without the spatial coordinates:

This is because in the formula for the axisymmetric case, the component of the strain is computed as , where is the first dependent variable and the radial direction in the cylindrical coordinate system. The derivation is given in the section Axisymmetric Models. When the stress is computed from the strains, the value for is taken from the first given displacement function, usol in this case. If that function does not depend on the independent variables and , then they cannot appear in the output.