VonMisesStress[vars,pars,stress]
yields the vonMises stress from stress.


VonMisesStress
VonMisesStress[vars,pars,stress]
yields the vonMises stress from stress.
Details

- The von Mises stress measure is used to anticipate if a ductile material under stress will yield.
- The von Mises stress is also known as maximum distortion energy.
- The units of the von Mises stress
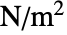 are a pressure [
are a pressure [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/VonMisesStress.en/3.png) ].
]. - VonMisesStress uses the same variables vars specification as SolidMechanicsPDEComponent.
- VonMisesStress uses the same parameter pars specification as SolidMechanicsPDEComponent.
- stress is specified through a SymmetrizedArray.
- Typically, the stress SymmetrizedArray is of dimension 3 by 3 and has to be symmetric.
- Typically, stress is the result of SolidMechanicsStress.
- VonMisesStress computes:
- The
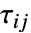 represent normal stresses and
represent normal stresses and  represent shear stresses.
represent shear stresses.
Examples
open all close allBasic Examples (2)
Compute the von Mises stress of a stress tensor:
Compute if a load on a beam will be beyond the yield limit of the material. Create the beam:
Set up the variables and material parameters:
The beam is held fixed at the left and and a load of 100 newtons in the downward direction is applied at the right end of the beam. Compute the displacement of the beam under a load:
Compute the strain and stress from the displacement:
Visualize the von Mises stress:
Find the maximal von Mises stress value:
Check if the maximal von Mises stress is smaller than the yield strength of the material:
Scope (3)
Express the von Mises stress through strain. Compute stress from a strain:
Express the von Mises stress through displacement. Compute the strain from a displacement:
Explore a failure criterion based on the von Mises stress for a titanium beam-like structure.
Set up the geometry of the beam:
Set up variables and material parameters:
Compute the strains from the displacement:
Compute the stresses from the strains:
Compute the von Mises stress from the stress tensor:
Visualize the von Mises stress intensity over the deformed body:
To find those areas in the beam that are subject to failure, apply a criterion on the values of the von Mises stress with respect to the yielding limit of the material. Find the tensile yield strength of the material:
Only the regions with stress higher than the limit value may be subjected to failure:
Applications (5)
Stationary Analysis (2)
Compute the deflection of a spoon held fixed at the end and with a force applied at the top. Set up variables and parameters:
Set up the PDE and the geometry:
Compute the strains from the displacement:
Compute the stresses from the strains:
Compute the von Mises stress from the stress tensor:
Visualize the von Mises stress:
Explore a failure criterion based on the von Mises stress for a titanium fixation plate used for orthopedic surgery subjected to torque.
Set up the geometry of a typical forearm fixation plate:
Set up variables and material parameters:
The plate is 16×1×0.3 ![]() with several holes. Consider a setup where the first quarter is held fixed and the last quarter is subject to a torque:
with several holes. Consider a setup where the first quarter is held fixed and the last quarter is subject to a torque:
Compute the strains from the displacement:
Compute the stresses from the strains:
Compute the von Mises stress from the stress tensor:
Visualize the von Mises stress intensity over the deformed body:
To find those areas in the fixation plate that are subject to failure, apply a criterion on the values of the von Mises stress with respect to the yielding limit of the material. Find the tensile yield strength of the material:
Only the regions with stress higher than the limit value may be subjected to failure:
Hyperelastic Stationary Analysis (2)
Compute the von Mises stress in an object with a hyperelastic material. Set up variables and material properties:
The geometry is held fixed on the left edge and pulled to the right on the right edge. Solve the PDE for the displacement:
Compute the strains from the displacement:
Compute the stresses from strains and displacements:
Compute the von Mises stress from the stress tensor:
Visualize the von Mises stress in the to-scale deformed object:
Compute the von Mises stress in an 3D object with a hyperelastic material. Set up variables and material properties:
The geometry is held fixed on the left edge and pulled to the right on the right edge. Solve the PDE for the displacement with a coarse mesh:
Compute the strains from the displacement:
Compute the stresses from strains and displacements and measure the time it takes:
Compute the von Mises stress from the stress tensor:
Visualize the von Mises stress in the to-scale deformed object:
Fiber-Reinforced Hyperelastic Stationary Analysis (1)
Set up the variables and the model parameters for a fiber-reinforced piece of rubber that is held fixed at the left and a pressure is applied on the right. A neo-Hookean hyperelastic material model is used:
Visualize the fiber reinforcement in the geometry:
Set up the equation and solve for the displacement:
Visualize the deformed body over the original shape of the body:
Possible Issues (1)
A 2 by 2 stress tensor can be used:
Caution is in order here as, for example, in a plane strain case there may still be nonzero stresses in the third direction. This is explained in the section "Plane Strain, Plane Stress and Axisymmetric Models" of the solid mechanics monograph. It is, however, possible to use a two-dimensional variable setup with a 3 by 3 stress tensor:
Tech Notes
Related Guides
Text
Wolfram Research (2024), VonMisesStress, Wolfram Language function, https://reference.wolfram.com/language/ref/VonMisesStress.html (updated 2025).
CMS
Wolfram Language. 2024. "VonMisesStress." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/VonMisesStress.html.
APA
Wolfram Language. (2024). VonMisesStress. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VonMisesStress.html
BibTeX
@misc{reference.wolfram_2025_vonmisesstress, author="Wolfram Research", title="{VonMisesStress}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/VonMisesStress.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_vonmisesstress, organization={Wolfram Research}, title={VonMisesStress}, year={2025}, url={https://reference.wolfram.com/language/ref/VonMisesStress.html}, note=[Accessed: 11-March-2026]}