Sphere

Sphere[p]

点 p を中心とした単位球を表す．

Sphere[p,r]

点 p を中心とした半径 r の球を表す．

Sphere[{p1,p2,…},r]

半径 r の球の集合を表す．

詳細とオプション

  • Sphereは，幾何学領域として，またグラフィックスプリミティブとして使うことができる．
  • Sphere[]はSphere[{0,0,0}]に等しい． »
  • Sphere[n]は，正の整数 n については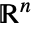，の単位球，Sphere[{0,…,0}]に等しい．
  • Sphereは外郭構造{x|TemplateBox[{{x, -, p}}, Norm]=r}を表す．
  • Sphereは，GraphicsおよびGraphics3Dで使うことができる．
  • グラフィックスでは，点 p, piおよび半径 r は，Scaled式およびDynamic式でよい．
  • グラフィックスの描画は，FaceForm，Specularity，Opacity，色の各指示子の影響を受ける．
  • Sphere[{p1,p2,…},{r1,r2,…}]は，中心 pi，半径 riの球の集合を表す．

予備知識

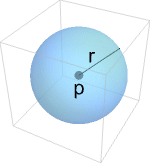
  • Sphereは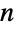， 次元空間にある球面を表すグラフィックスおよび幾何のプリミティブである．Sphere[p,r]は，TemplateBox[{}, Reals]^nにおける，中心 p，半径 r の球面{x:TemplateBox[{{x, -, p}}, Norm]=r}を表す．r は任意の非負の実数でよく，p は任意の正の長さ 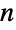でよい．略記形式のSphere[p]はSphere[p,1]に，Sphere[n]はSphere[ConstantArray[0, n],1]に等しく，Sphere[]は自動評価されてSphere[{0,0,0}]となる．
  • 半径 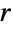が等しい球面オブジェクトの集合（複数の球面）は，Sphere[{p1,…,pk},r]によって効率的に表すことができ，半径が異なる球はSphere[{p1,…,pk},{r1,…,rk}]によって表すことができる．
  • Sphereオブジェクトは，GraphicsおよびGraphics3Dを使って，それぞれ二次元および三次元で視覚的にフォーマットすることができる．グラフィックス内のSphereオブジェクトの外観は，面指示子FaceForm（三次元），Redのような色指示子，不透明度／透明度の指示子のOpacity／Specularity，スタイルオプションのAntialiasingを使って変更することができる．
  • Sphereは，計算を行うべき領域指定にも使うことができる．例えば，Integrate[1,{x,y,z}∈Sphere[{0,0,0},r]]とArea[Sphere[{0,0,0},r]]はどちらも半径 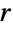の球の表面積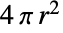を返す．
  • Sphereは数多くの他のシンボルと関連がある．Sphereは，RegionBoundary[Ball[{x,y,z},r]]を使って計算できるように，球体の境界を表す．楕円体の表面積（Ellipsoidで表される立体としての楕円体と混同してはならない）は，Scaledを使ってSphereから求めることができる．与えられた点集合を通る球面はCircumsphereを使って得ることができる．Sphereオブジェクトは，ImplicitRegion[(x-u)2+(y-v)2+(z-w)2r2,{u,v,w}]または ParametricRegion[{x,y,z}+r{Cos[θ]Sin[ϕ],Sin[θ]Sin[ϕ],Cos[ϕ]},{{θ,0,2π},{ϕ,0,π}}]として表すことができる．SurfaceData["Sphere",property]あるいはEntity["Surface","Sphere"][property]を使って標準位置にある球面の計算済みの特性を得ることができる．

例題

すべて開くすべて閉じる

例  (2)

原点における単位球：

面積と重心：

スコープ  (22)

グラフィックス  (12)

指定  (4)

単位球：

半径の異なる球：

原点における単位球の短縮形：

複数の球：

スタイリング  (4)

色付きの球：

FaceFormを使って表面と裏面に異なる特性を指定することができる：

異なる鏡面反射指数の球：

赤く輝く黒い球：

Opacityは表面の不透明度を指定する：

座標  (4)

Scaled座標を使う：

Scaled半径を使う：

通常の座標からスケールされたオフセットを指定する：

点はDynamicでもよい：

領域  (10)

埋込み次元は，球がある空間の次元である：

幾何次元は形それ自身の次元である：

帰属判定：

点の帰属条件を得る：

面積：

重心：

点からの距離：

球の等距離等高線：

点からの符号付き距離：

領域内の最近点：

包み込んでいる球までの最近点：

球は有界である：

その範囲を求める：

球領域で積分する：

球領域で最適化する：

球領域で方程式を解く：

アプリケーション  (5)

球で表されたプラトンの多面体：

二重螺線：

泡：

Sphereを使ってGraphPlot3Dのノードを描画する：

BubbleChart3DでSphereを使う：

特性と関係  (8)

Scaleを使って楕円体を得る：

Sphereの2DバージョンはCircleである：

ContourPlot3Dで生成された球の陰的指定：

ParametricPlot3Dで生成された球のパラメータ的な指定：

ChemicalDataは球と円柱を使って分子をプロットする：

Import形式のいくつかは分子を表すのに球を使う：

Circumsphereは球面上の点からSphereを指定する：

ImplicitRegionは任意のSphereを表すことができる：

おもしろい例題  (4)

ランダムな球の集合：

球による立方格子：

球によるBCC格子：

NIntegrateで使われたサンプル点：

Wolfram Research (2007), Sphere, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sphere.html （2014年に更新）.

テキスト

Wolfram Research (2007), Sphere, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sphere.html （2014年に更新）.

CMS

Wolfram Language. 2007. "Sphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Sphere.html.

APA

Wolfram Language. (2007). Sphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sphere.html

BibTeX

@misc{reference.wolfram_2024_sphere, author="Wolfram Research", title="{Sphere}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Sphere.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sphere, organization={Wolfram Research}, title={Sphere}, year={2014}, url={https://reference.wolfram.com/language/ref/Sphere.html}, note=[Accessed: 21-November-2024 ]}